题目内容
点P为椭圆
+
=1(a>0,b>0)在第一象限的弧上任意一点,过P引x轴,y轴的平行线,分别交直线y=-
x于Q、R,交y轴、x轴于M、N两点,记△OMQ与△ONR的面积分别为S1,S2,当ab=2时,S12+S22的最小值为 .
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设设P点的坐标为(n,m),(n>0,m>0),由题意分别表示出Q、R,M、N的坐标,再求出S1,S2的面积,再根据点P再椭圆上,利用基本不等式求得mn≤1,
再利用基本不等式求出S12+S22≥2S1•S2≥
,问题得以解决
再利用基本不等式求出S12+S22≥2S1•S2≥
| 1 |
| 2 |
解答:
 解:设P点的坐标为(n,m),(n>0,m>0)
解:设P点的坐标为(n,m),(n>0,m>0)
∵过P引x轴,y轴的平行线,分别交直线y=-
x于Q、R,交y轴、x轴于M、N两点,
∴点Q的坐标为(-
,m),点R的坐标为(n,-
),点M的坐标为(0,m),点N的坐标为(n,0),
∴|NR|=
,|ON|=n,|MQ|=
,|OM|=m,
∴S1=S△OMQ=
×m×
=
,S2=S△ONR=
×n×
=
,
∴S1•S2=
,
∵P点在椭圆
+
=1上,
∴
+
=1,
∴1=
+
≥2•
=mn,
即mn≤1,
∴S12+S22≥2S1•S2=
≥
,
故S12+S22的最小值为
故答案为:
 解:设P点的坐标为(n,m),(n>0,m>0)
解:设P点的坐标为(n,m),(n>0,m>0)∵过P引x轴,y轴的平行线,分别交直线y=-
| b |
| a |
∴点Q的坐标为(-
| am |
| b |
| bn |
| a |
∴|NR|=
| bn |
| a |
| am |
| b |
∴S1=S△OMQ=
| 1 |
| 2 |
| am |
| b |
| am2 |
| 2b |
| 1 |
| 2 |
| bn |
| a |
| bn2 |
| 2a |
∴S1•S2=
| m2n2 |
| 4 |
∵P点在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴
| n2 |
| a2 |
| m2 |
| b2 |
∴1=
| n2 |
| a2 |
| m2 |
| b2 |
| nm |
| ab |
即mn≤1,
∴S12+S22≥2S1•S2=
| m2n2 |
| 2 |
| 1 |
| 2 |
故S12+S22的最小值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了椭圆的有关知识,以及基本不等式的应用,培养了学生的转化能力,运算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则椭圆中心的轨迹方程是( )
A、(x-
| ||||
B、(x+
| ||||
C、x2+(y-
| ||||
D、x2+(y+
|
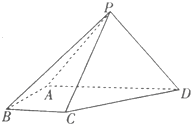 如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=