题目内容
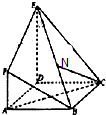 如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.(Ⅰ)证明:BE⊥AC;
(Ⅱ)点N在棱BE上,当BN的长度为多少时,直线CN与平面ADE成30°角.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得DE⊥平面ABCD,DA、DE、DC两两互相垂直,建立空间直角坐标系,利用向量法能证明BE⊥AC.
(Ⅱ)设
=λ
,0≤λ≤1,则
=
+
=
+λ
=(-2λ+2,-2λ,2λ),
为平面ADE的法向量,由此利用向量法能求出BN的长.
(Ⅱ)设
| BN |
| BE |
| CN |
| CB |
| BN |
| CB |
| BE |
| CD |
解答:
(Ⅰ)证明:∵AF⊥平面ABCD,DE∥AF,
∴DE⊥平面ABCD,
又∵ABCD是正方形,∴DA、DE、DC两两互相垂直,
建立如图所示的空间直角坐标系,
由已知得A(2,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
=(-2,2,0),
=(-2,-2,2),
∴
•
=4-4+0=0,∴BE⊥AC.
(Ⅱ)解:
=(2,0,0),
=(-2,-2,2),
=(0,-2,0),
∵点N在棱BE上,∴设
=λ
,0≤λ≤1,
∴
=
+
=
+λ
=(-2λ+2,-2λ,2λ),
∵CD⊥平面ADE,∴
为平面ADE的法向量,
当直线CN与平面ADE成30°角时,<
,
>=60°,
∴cos<
,
>=
=cos60°=
,
解得λ=-1±
,
∵0≤λ≤1,∴λ=
-1,
∴BN的长为|
|=λ|
|=(
-1)•2
=2
-2
.

∴DE⊥平面ABCD,
又∵ABCD是正方形,∴DA、DE、DC两两互相垂直,
建立如图所示的空间直角坐标系,
由已知得A(2,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
| AC |
| BE |
∴
| AC |
| BE |
(Ⅱ)解:
| CB |
| BE |
| CD |
∵点N在棱BE上,∴设
| BN |
| BE |
∴
| CN |
| CB |
| BN |
| CB |
| BE |
∵CD⊥平面ADE,∴
| CD |
当直线CN与平面ADE成30°角时,<
| CN |
| CD |
∴cos<
| CN |
| CD |
| λ | ||
|
| 1 |
| 2 |
解得λ=-1±
| 2 |
∵0≤λ≤1,∴λ=
| 2 |
∴BN的长为|
| BN |
| BE |
| 2 |
| 3 |
| 6 |
| 3 |
点评:本题考查线线垂直、线面垂直、线面角、空间向量的应用等基础知识,考查空间想象能力、运算求解能力、推理论证能力和探究能力.

练习册系列答案
相关题目
已知A={x|x2-4x+3≥0},B={x|x≤0或x≥4},则( )
| A、A?B | B、B?A |
| C、A=B | D、A∩B=∅ |
以两条坐标轴为对称轴的椭圆过点P(
,-4)和Q(-
,3),则此椭圆的方程是( )
| 3 |
| 5 |
| 4 |
| 5 |
A、
| ||||
B、x2+
| ||||
C、
| ||||
| D、以上均不对 |
过原点的椭圆的一个焦点为F(1,0),其长轴长为4,则椭圆中心的轨迹方程是( )
A、(x-
| ||||
B、(x+
| ||||
C、x2+(y-
| ||||
D、x2+(y+
|
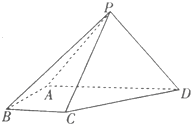 如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=