题目内容
已知数列{an}，an=23n-1，求前n项和Sn．
考点：数列的求和
专题：等差数列与等比数列
分析：首项证明数列是等比数列，进一步利用数列的前n项和公式求出结果．
解答：
解：数列{an}，an=23n-1，
则：
=
=23（常数）
所以{an}是以a1为首，23为公比的等比数列．
Sn=
=
(23n-1)
则：
| an+1 |
| an |
| 23n+2 |
| 23n-1 |
所以{an}是以a1为首，23为公比的等比数列．
Sn=
| a1-anq |
| 1-q |
| 4 |
| 7 |
点评：本题考查的知识要点：等比数列的定义，等比数列的前n项和公式的应用．属于基础题型．
练习册系列答案
教材全解字词句篇系列答案
相关题目
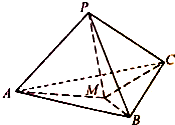如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
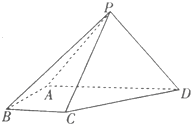如图，在四棱锥P-ABCD中，BA⊥侧面PAD，侧棱PA=PD=