题目内容

16．高二年级有男生560人，女生420人，为了解学生职业规划，现用分层抽样的方法从该年级全体学生中抽取一个容量为280人的样本，则此样本中男生人数为（　　）
A．120B．160C．280D．400

分析 先根据男生和女生的人数做出年纪大总人数，用要抽取得人数除以总人数得到每个个体被抽到的概率，用男生人数乘以概率，得到结果．

解答 解：∵有男生560人，女生420人，
∴年级共有560+420=980，
∵用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本，
∴每个个体被抽到的概率是$\frac{280}{980}$=$\frac{2}{7}$，
∴要从男生中抽取560×$\frac{2}{7}$=160，
故选：B．

点评 本题考查分层抽样方法，本题解题的关键是在抽样过程中每个个体被抽到的概率相等，这是解题的依据，本题是一个基础题．

练习册系列答案
相关题目
6．抛物线 M：y2=2px（p＞0）与椭圆 $N：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$有相同的焦点F，抛物线M与 椭圆N交于A，B，若F，A，B共线，则椭圆N的离心率等于$\sqrt{2}$-1．
7．已知函数f（x）=$\left\{\begin{array}{l}{-lnx，x≥0}\\{（\frac{1}{2}）^{x}，x＜0}\end{array}\right.$则f（f（e））=2．
4．在△ABC中，a、b、c分别为A、B、C所对的边，且2acosB+bcosA=2c，则△ABC是（　　）
A．锐角三角形B．钝角三角形C．直角三角形D．斜三角形
11．已知，在△ABC中，a、b、c分别为角A、B、C的对边，且asinB=$\sqrt{3}$bcosA．
（1）求角A的大小；
（2）设△ABC的面积为$\sqrt{3}$，求a的取值范围．
1．已知两个圆O1和O2，它们的半径分别是2和4，且|O1O2|=8，若动圆M与圆O1内切，又与O2外切，则动圆圆心M的轨迹方程是（　　）
A．圆B．椭圆C．双曲线一支D．抛物线
8．设点M（3，t），若在圆O：x2+y2=6上存在两点A，B，使得∠AMB=90°，则t的取值范围是-$\sqrt{3}$≤t≤$\sqrt{3}$．
5．命题p：?x∈R，2${\;}^{{x}^{2}-1}$＜$\frac{1}{4}$，命题q：若M为曲线y2=4x2上一点，A（$\frac{5}{2}$，0），则|MA|的最小值为$\sqrt{5}$，那么下列命题为真命题的是（　　）
A．（￢p）∧（￢q）B．p∨（￢q）C．p∧（￢q）D．（￢p）∧q
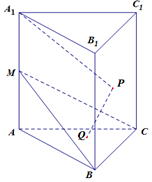6．如图，在棱长均为2的正三棱柱ABC-A1B1C1中，点M是侧棱AA1的中点，点P、Q分别是侧面BCC1B1、底面ABC内的动点，且A1P∥平面BCM，PQ⊥平面BCM，则点Q的轨迹的长度为$\frac{4}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网