题目内容
4.在△ABC中,a、b、c分别为A、B、C所对的边,且2acosB+bcosA=2c,则△ABC是( )| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
分析 由正弦定理化简已知可得2sinAcosB+sinBcosA=2sinC,由三角形内角和定理,两角和的正弦函数公式可得
2sinC=2sinAcosB+2sinBcosA,解得sinBcosA=0,由sinB≠0,可求cosA=0,结合范围A∈(0,π),可得A的值.
解答 解:∵△ABC中,2acosB+bcosA=2c,
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,得:2sinAcosB+sinBcosA=2sinC
又∵2sinC=2sin(A+B)=2sinAcosB+2sinBcosA,
∴sinBcosA=2sinBcosA,可得:sinBcosA=0,
∵sinB≠0,
∴可得:cosA=0,
∴由A∈(0,π),可得:A=$\frac{π}{2}$.
故选:C.
点评 本题考查三角形的形状判断,着重考查正弦定理,三角形内角和定理,两角和的正弦函数公式的应用,属于基础题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
19.已知命题p:?x∈R,x2-x+1≤0,则( )
| A. | ¬p:?x0∈R,x02-x0+1≤0 | B. | ¬p:?x∈R,x2-x+1≥0 | ||
| C. | ¬p:?x∈R,x2-x+1>0 | D. | ¬p:?0x∈R,x02-x0+1>0 |
16.高二年级有男生560人,女生420人,为了解学生职业规划,现用分层抽样的方法从该年级全体学生中抽取一个容量为280人的样本,则此样本中男生人数为( )
| A. | 120 | B. | 160 | C. | 280 | D. | 400 |
13.命题:“若$\sqrt{x}$>1,则lnx>0”的否命题为( )
| A. | 若$\sqrt{x}$>1,则lnx≤0 | B. | 若$\sqrt{x}$≤1,则lnx>0 | C. | 若$\sqrt{x}$≤1,则lnx≤0 | D. | 若lnx>0,则$\sqrt{x}$>1 |
14.抛物线y=9x2的焦点坐标为( )
| A. | ($\frac{1}{36}$,0) | B. | (0,$\frac{1}{36}$) | C. | ($\frac{9}{4}$,0) | D. | (0,$\frac{9}{4}$) |
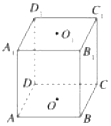 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条. 在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.
在如图所示的几何体中,四边形DCFE为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,且AC⊥FB.