题目内容
6.抛物线 M:y2=2px(p>0)与椭圆 $N:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$有相同的焦点F,抛物线M与 椭圆N交于A,B,若F,A,B共线,则椭圆N的离心率等于$\sqrt{2}$-1.分析 由题意可知:AF⊥x轴,$\frac{p}{2}$=c,代入抛物线方程即可求得A点坐标,代入椭圆方程,利用离心率公式即可求得椭圆N的离心率.
解答 解:如图所示由F,A,B共线,
则AF⊥x轴,
由抛物线 M:y2=2px(p>0)与椭圆 $N:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$有相同的焦点F,
∴$\frac{p}{2}$=c,
把x=$\frac{p}{2}$,代入抛物线方程可得:y2=2p•$\frac{p}{2}$,解得:y=p.
∴A($\frac{p}{2}$,p),即A(c,2c).
代入椭圆的方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{4{c}^{2}}{{b}^{2}}=1$,
又b2=a2-c2,
∴$\frac{{c}^{2}}{{a}^{2}}+\frac{4{c}^{2}}{{a}^{2}-{c}^{2}}=1$,由椭圆的离心率e=$\frac{c}{a}$,
整理得:e4-6e2+1=0,0<e<1.
解得:e2=3-2$\sqrt{2}$,
∴e=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查椭圆的标准方程及简单几何性质,考查椭圆的离心率公式,考查数形结合思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.圆x2+y2=1与圆(x-2)2+(y-2)2=5的位置关系为( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
1.已知{an}是等比数列,且 ${a_5}=\frac{1}{2},4{a_3}+{a_7}=2$,则a9=( )
| A. | 2 | B. | ±2 | C. | 8 | D. | $\frac{1}{8}$ |
18.已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,过F作倾斜角为60°的直线l,直线l与双曲线交于A,与y轴交于点B,且$\overrightarrow{FA}$=$\frac{1}{2}$$\overrightarrow{FB}$,则该双曲线的离心率等于( )
| A. | $\sqrt{3}$+1 | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\frac{\sqrt{3}}{2}$+1 | D. | $\frac{\sqrt{3}-1}{4}$ |
16.高二年级有男生560人,女生420人,为了解学生职业规划,现用分层抽样的方法从该年级全体学生中抽取一个容量为280人的样本,则此样本中男生人数为( )
| A. | 120 | B. | 160 | C. | 280 | D. | 400 |
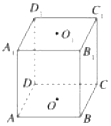 如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.
如图所示,在正方体ABCD-A1B1C1D1中,O1、O为上、下底面的中心,在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条.