题目内容

6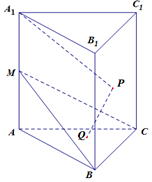．如图，在棱长均为2的正三棱柱ABC-A1B1C1中，点M是侧棱AA1的中点，点P、Q分别是侧面BCC1B1、底面ABC内的动点，且A1P∥平面BCM，PQ⊥平面BCM，则点Q的轨迹的长度为$\frac{4}{3}$．

分析 根据已知可得点Q的轨迹是过△MBC的重心，且与BC平行的线段，进而根据正三棱柱ABC-A1B1C1中棱长均为2，可得答案．

解答 解：∵点P是侧面BCC1B1内的动点，且A1P∥平面BCM，
则P点的轨迹是过A1点与平面MBC平行的平面与侧面BCC1B1的交线，
则P点的轨迹是连接侧棱BB1，CC1中点的线段l，
∵Q是底面ABC内的动点，且PQ⊥平面BCM，
则点Q的轨迹是过l与平面MBC垂直的平面与平面MBC的线段m，

故线段m过△MBC的重心，且与BC平行，
由正三棱柱ABC-A1B1C1中棱长均为2，
故线段m的长为：$\frac{2}{3}$×2=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$

点评 本题考查的知识点是平面与平面之间的位置关系，棱柱的几何特征，动点的轨迹，难度中档．

练习册系列答案
相关题目
16．高二年级有男生560人，女生420人，为了解学生职业规划，现用分层抽样的方法从该年级全体学生中抽取一个容量为280人的样本，则此样本中男生人数为（　　）
A．120B．160C．280D．400
17．定义在R上的偶函数f（x）满足，当x＜0时，f（x）=$\frac{x}{x-1}$，则曲线y=f（x）在点（2，f（2））处的切线的斜率为$\frac{1}{9}$．
14．抛物线y=9x2的焦点坐标为（　　）
A．（$\frac{1}{36}$，0）B．（0，$\frac{1}{36}$）C．（$\frac{9}{4}$，0）D．（0，$\frac{9}{4}$）
1．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，点M在双曲线C1的一条渐近线上，且OM⊥MF2，若△OMF2的面积为16，且双曲线C1与双曲线C2：$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1的离心率相同，则双曲线C1的实轴长为（　　）
A．32B．16C．8D．4
11．圆（x-1）2+y2=1的圆心和半径分别为（　　）
A．（0，1），1B．（0，-1），1C．（-1，0），1D．（1，0），1
18．将边长为2的正方形ABCD沿对角线AC折起，使得BD=2，则三棱锥D-ABC的顶点D到底面ABC的距离为$\sqrt{2}$．
15．已知直线l过坐标原点O，圆C的方程为x2+y2-6y+4=0．
（Ⅰ）当直线l的斜率为$\sqrt{2}$时，求l与圆C相交所得的弦长；
（Ⅱ）设直线l与圆C交于两点A，B，且A为OB的中点，求直线l的方程．
16．向量$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，2），则$\overrightarrow{a}$-2$\overrightarrow{b}$的模等于$\sqrt{17}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网