题目内容
已知函数y=sin
ωx在(0,π)内是减函数,则ω的取值范围为 .
| 1 |
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由周期公式求出函数的周期,再根据正弦函数的单调区间的长度和条件列出不等式,求出ω的取值范围.
解答:
解:函数y=sin
ωx的周期T=
=
,
∵在(0,π)内是减函数,
∴
≥π,即
≥π,解得0<ω≤1或-1≤ω<0,
故答案为:0<ω≤1或-1≤ω<0.
| 1 |
| 2 |
| 2π | ||
|
| 4π |
| |ω| |
∵在(0,π)内是减函数,
∴
| T |
| 2 |
| 2π |
| |ω| |
故答案为:0<ω≤1或-1≤ω<0.
点评:本题考查了正弦函数的单调性与周期性和关系,以及周期公式的应用,关键是掌握正弦函数曲线的变化规律,注意ω的范围,属于中档题.

练习册系列答案
相关题目
已知直线l1:ax-2y-1=0,l2:6x-4y+1=0,若l1∥l2,则实数a的值是( )
| A、1 | B、2 | C、3 | D、4 |
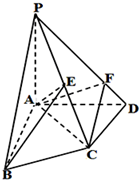 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3