题目内容
设实数x,y满足
+
=1,则x+y的最小值是 .
| x2 |
| 6 |
| y2 |
| 3 |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:令t=x+y,联立
,消掉y后得关于x的二次方程,令△≥0可求t的范围.
|
解答:
解:令t=x+y,
由
,得3x2-4tx+2t2-6=0,
则△=16t2-4×3(2t2-6)≥0,解得-3≤t≤3,
∴x+y的最小值为-3,
故答案为:-3.
法二:令x=
cosθ,y=
sinθ
∴x+y=
sinθ+
cosθ
=
sin(θ+α)
∴x+y的最小值为-3,
由
|
则△=16t2-4×3(2t2-6)≥0,解得-3≤t≤3,
∴x+y的最小值为-3,
故答案为:-3.
法二:令x=
| 6 |
| 3 |
∴x+y=
| 3 |
| 6 |
=
| 6+3 |
∴x+y的最小值为-3,
点评:该题考查函数最值的求解、不等式的解法,属基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
任取一自然数,则该数平方的未位数是6的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
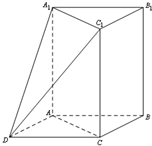 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.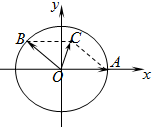 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若