题目内容
已知某种同型号的6瓶饮料中有2瓶已过了保质期.
(1)从6瓶饮料中任意抽取1瓶,求抽到没过保质期的饮料的概率;
(2)从6瓶饮料中随机抽取2瓶,求抽到已过保质期的饮料的概率.
(1)从6瓶饮料中任意抽取1瓶,求抽到没过保质期的饮料的概率;
(2)从6瓶饮料中随机抽取2瓶,求抽到已过保质期的饮料的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)从6瓶饮料中任意抽取1瓶的基本事件个数为
.从没过保质期的饮料中任意抽取1瓶的基本事件个数为
.从而得到从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率为
.
(2)从6瓶饮料中任意抽取2瓶的基本事件个数为
.从已过保质期的饮料中任意抽取2瓶的基本事件个数为
-
.从而得到从6瓶饮料中随机抽取2瓶,抽到已过保质期的饮料的概率为
.
| C | 1 6 |
| C | 1 4 |
| 2 |
| 3 |
(2)从6瓶饮料中任意抽取2瓶的基本事件个数为
| C | 2 6 |
| C | 2 6 |
| C | 2 4 |
| 3 |
| 5 |
解答:
解:(1)∵从6瓶饮料中任意抽取1瓶的基本事件个数为
.
从没过保质期的饮料中任意抽取1瓶的基本事件个数为
.
∴从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率
P=
=
.
(2)∵从6瓶饮料中任意抽取2瓶的基本事件个数为
.
从已过保质期的饮料中任意抽取2瓶的基本事件个数为
-
.
∴从6瓶饮料中随机抽取2瓶,抽到已过保质期的饮料的概率为
P=
=
=
.
| C | 1 6 |
从没过保质期的饮料中任意抽取1瓶的基本事件个数为
| C | 1 4 |
∴从6瓶饮料中任意抽取1瓶,抽到没过保质期的饮料的概率
P=
| ||
|
| 2 |
| 3 |
(2)∵从6瓶饮料中任意抽取2瓶的基本事件个数为
| C | 2 6 |
从已过保质期的饮料中任意抽取2瓶的基本事件个数为
| C | 2 6 |
| C | 2 4 |
∴从6瓶饮料中随机抽取2瓶,抽到已过保质期的饮料的概率为
P=
| ||||
|
| 15-6 |
| 15 |
| 3 |
| 5 |
点评:本题考查古典概型及概率计算公式等知识,属于基础题.

练习册系列答案
相关题目
“函数y=sin(x+φ)为偶函数”是“φ=
”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
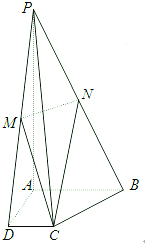 如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
如图,四棱锥P-ABCD,PA⊥平面ABCD,且PA=4,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,
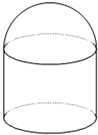 如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
如图,储油灌的表面积S为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.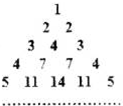 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn. 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,