题目内容
已知数列{an}满足a1=1,an=a1+
a2+…+
an-1(n>1),则数列{an}的通项公式an= .
| 1 |
| 2 |
| 1 |
| n-1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:根据递推数列构造新数列,利用作差法即可得到数列{an}的通项公式an.
解答:
解:∵an=a1+
a2+…+
an-1(n>1),
∴an+1=a1+
a2+…+
an-1+
an,
两式相减得an+1-an=
an,
即an+1=
an,
即
=
,
=
,…,
=
,
等式两边同时相乘得
=
,
即an=
a2,(n≥2),
当n=1时,a1=1,
当n=2时,a2=a1=1,
∴an=
a2=
,(n≥2),
即an=
.
故答案为:an=
.
| 1 |
| 2 |
| 1 |
| n-1 |
∴an+1=a1+
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n |
两式相减得an+1-an=
| 1 |
| n |
即an+1=
| n+1 |
| n |
即
| a3 |
| a2 |
| 3 |
| 2 |
| a4 |
| a3 |
| 4 |
| 3 |
| an |
| an-1 |
| n |
| n-1 |
等式两边同时相乘得
| an |
| a2 |
| n |
| 2 |
即an=
| n |
| 2 |
当n=1时,a1=1,
当n=2时,a2=a1=1,
∴an=
| n |
| 2 |
| n |
| 2 |
即an=
|
故答案为:an=
|
点评:本题主要考查数列{an}的通项公式的求解,利用递推公式构造新的方程是解决本题的关键,考查学生的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从2名男生和2名女生中,任意选择两人在星期六、星期日参加某公益活动,每天一人,则星期六安排一名男生、星期日安排一名女生的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
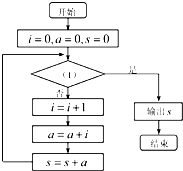 在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是
在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是