Question

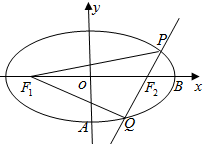已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦距为2

2

，设F₁、F₂为椭圆的左、右焦点，过F₂作直线交椭圆于P、Q两点，且△PF₁Q的周长为4

3

．
（1）求椭圆的方程；
（2）设△PQF₁的面积为

3

，求直线PQ的斜率．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知条件推导出2c=2

2

，4a=4

3

，由此能求出椭圆的方程．
（2）设直线PQ的斜率为k，则直线PQ：y=k(x-

2

)，联立

y=k(x- 2 ) x2 3 +y2=1

，得（1+3k²）x-6

2

k²x+6k²-3=0，由椭圆弦长公式和点到直线的距离公式能求出直线PQ的斜率．

解答： 解：（1）∵椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦距为2

2

，
∴2c=2

2

，解得c=

2

，（1分）
∵F₁、F₂为椭圆的左、右焦点，过F₂作直线交椭圆于P、Q两点，且△PF₁Q的周长为4

3

，
∴4a=4

3

，解得a=

3

，（2分）
∴b²=3-2=1，
∴椭圆的方程为

x2

3

+y2=1．（4分）
（2）设直线PQ的斜率为k，
∵F2(

2

，0)，∴直线PQ：y=k(x-

2

)，
联立

y=k(x- 2 ) x2 3 +y2=1

，得（1+3k²）x-6

2

k²x+6k²-3=0，（5分）
设P（x₁，y₁），Q（x₂，y₂），
则△＞0，x₁+x₂=

6 2 k2

1+3k2

，x1x2=

6k2-3

1+3k2

，
F₁（-

2

，0）到直线PQ的距离d=

|- 2 k- 2 k|

k2+1

=

2 2 |k|

k2+1

，（6分）
∵△PQF₁的面积为

3

，
∴

1

2

d•|PQ|=

2 |k|

k2+1

(1+k2)[( 6 2 k2 1+3k2 )2-4× 6k2-3 1+3k2 ]

=

3

，（8分）
解得k=±1．（10分）

点评：本题考是椭圆方程的求法，考查直线的斜率的求法，是中档题，解题时要注意椭圆弦长公式和点到直线的距离公式的灵活运用．