题目内容
已知函数f(x)=(x+1)ln(x+1)-ax2-x(a∈R),若对任意x>0,f(x)<0恒成立,求a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:导数的概念及应用,导数的综合应用
分析:若对任意x>0,f(x)<0恒成立,仅需函数f(x)=(x+1)ln(x+1)-ax2-x在(0,+∞)上递减即可,即f′(x)=ln(x+1)-2ax≤0在(0,+∞)上恒成立,即当x>0时,y=2ax的图象恒在y=ln(x+1)图象的上方,进而可得a的取值范围.
解答:
解:∵函数f(x)=(x+1)ln(x+1)-ax2-x,
∴f′(x)=ln(x+1)-2ax,
∵f(0)=0,
若对任意x>0,f(x)<0恒成立,
仅需函数f(x)=(x+1)ln(x+1)-ax2-x在(0,+∞)上递减即可,
即f′(x)=ln(x+1)-2ax≤0在(0,+∞)上恒成立,
即当x>0时,y=2ax的图象恒在y=ln(x+1)图象的上方,
由于y=2ax的图象与y=ln(x+1)图象交于(0,0)点,
故y=ln(x+1)的导数
<2a在x>0时恒成立,
由于g(x)=
在(0,+∞)上为减函数,且g(0)=1,
则2a≥1,
即a≥
,
故a的取值范围为:[
,+∞)
∴f′(x)=ln(x+1)-2ax,
∵f(0)=0,
若对任意x>0,f(x)<0恒成立,
仅需函数f(x)=(x+1)ln(x+1)-ax2-x在(0,+∞)上递减即可,
即f′(x)=ln(x+1)-2ax≤0在(0,+∞)上恒成立,
即当x>0时,y=2ax的图象恒在y=ln(x+1)图象的上方,
由于y=2ax的图象与y=ln(x+1)图象交于(0,0)点,
故y=ln(x+1)的导数
| 1 |
| x+1 |
由于g(x)=
| 1 |
| x+1 |
则2a≥1,
即a≥
| 1 |
| 2 |
故a的取值范围为:[
| 1 |
| 2 |
点评:本题考查的知识点是恒成立问题,利用导数分析函数的单调性,本题的转化比较复杂,属于难题.

练习册系列答案
相关题目
集合A={y|y=
+
},则A的真子集有( )个.
| sinx |
| |sinx| |
| |cosx| |
| cosx |
| A、4 | B、6 | C、7 | D、8 |
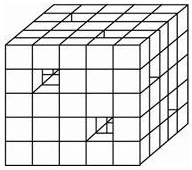 如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )| A、222 | B、258 |
| C、312 | D、324 |
已知⊙O:x2+y2=4,直线l:ax-y+1=0.则直线l与⊙O的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、与a的值有关 |
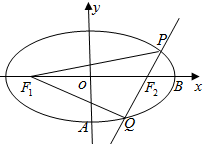 已知椭圆
已知椭圆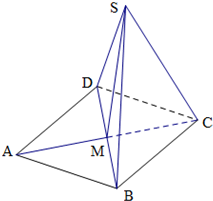 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.