题目内容
已知函数f(x)=
x2+
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式an;
(2)令bn=
,求数列{bn}的前n项和Tn;
(3)令cn=
+
,证明:c1+c2+…+cn>2n.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求数列{an}的通项公式an;
(2)令bn=
| an |
| 2n-1 |
(3)令cn=
| an |
| an+1 |
| an+1 |
| an |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件知Sn=
n2+
n,由此能求出an=n+1,n∈N*.
(2)bn=
=
,由此利用错位相减法能求出数列{bn}的前n项和Tn.
(3)cn=
+
=
+
,由此利用均值定理和放缩法能证明c1+c2+…+cn>2n.
| 1 |
| 2 |
| 3 |
| 2 |
(2)bn=
| an |
| 2n-1 |
| n+1 |
| 2n-1 |
(3)cn=
| an |
| an+1 |
| an+1 |
| an |
| n+1 |
| n+2 |
| n+2 |
| n+1 |
解答:
(1)解:∵函数f(x)=
x2+
x,数列{an}的前n项和为Sn,
点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴Sn=
n2+
n,
当n=1时,a1=S1=
+
=2.
当n≥2时,an=Sn-Sn-1=
n2+
n-[
(n-1)2+
(n-1)]=n+1,
当n=1时,也适合上式,
∴an=n+1,n∈N*.
(2)证明:由(1)得bn=
=
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②,得:
Tn=2+
+
+…+
-
=1+
-
=3-
-
,
∴Tn=6-
.
(3)cn=
+
=
+
≥2
=2,
∴c1+c2+…+cn>2(1+2+3+n)=2×
=n(n+1)>2n.
∴c1+c2+…+cn>2n.
| 1 |
| 2 |
| 3 |
| 2 |
点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴Sn=
| 1 |
| 2 |
| 3 |
| 2 |
当n=1时,a1=S1=
| 1 |
| 2 |
| 3 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当n=1时,也适合上式,
∴an=n+1,n∈N*.
(2)证明:由(1)得bn=
| an |
| 2n-1 |
| n+1 |
| 2n-1 |
∴Tn=
| 2 |
| 20 |
| 3 |
| 2 |
| 4 |
| 22 |
| n+1 |
| 2n-1 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+1 |
| 2n |
①-②,得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n+1 |
| 2n |
=1+
1×(1-
| ||
1-
|
| n+1 |
| 2n |
=3-
| 1 |
| 2n-1 |
| n+1 |
| 2n |
∴Tn=6-
| n+3 |
| 2n-1 |
(3)cn=
| an |
| an+1 |
| an+1 |
| an |
=
| n+1 |
| n+2 |
| n+2 |
| n+1 |
≥2
|
∴c1+c2+…+cn>2(1+2+3+n)=2×
| n(n+1) |
| 2 |
∴c1+c2+…+cn>2n.
点评:本题考查数列通项公式和前n项和公式的求法,考查不等式的证明,解题时要注意错位相减法和均值定理的合理运用.

练习册系列答案
相关题目
等比数列{an}的各项是正数,且a3a11=16,则a7=( )
| A、±4 | B、4 | C、±2 | D、2 |
已知⊙O:x2+y2=4,直线l:ax-y+1=0.则直线l与⊙O的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、与a的值有关 |
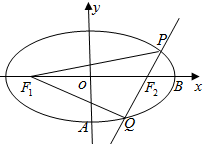 已知椭圆
已知椭圆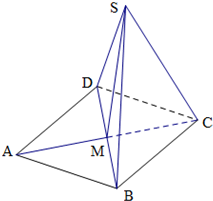 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.