题目内容
若（
+
）n的展开式中，各项系数的和与各项二项式系数的和之比为64，则n=（ ）
| x |
| 3 |
| x |
| A、4 | B、5 | C、6 | D、7 |
考点：二项式定理的应用
专题：二项式定理
分析：本题对于二项式系数的和可以通过赋值令x=1来求解，而各项二项式系数之和由二项式系数公式可知为2n，最后通过比值关系为64即可求出n的值．
解答：
解：令 （
+
）n中x为1得各项系数和为4n
又展开式的各项二项式系数和为2n
∵各项系数的和与各项二项式系数的和之比为64
∴
=64
解得n=6
故选：C．
| x |
| 3 |
| x |
又展开式的各项二项式系数和为2n
∵各项系数的和与各项二项式系数的和之比为64
∴
| 4n |
| 2n |
解得n=6
故选：C．
点评：本题考查求展开式的各项系数和的重要方法是赋值法、考查利用二项展开式的通项公式解决二项展开式的特定项问题，解答关键是利用展开式的各项的二项式系数的和为2n
练习册系列答案
相关题目
函数y=f（x）是定义在实数集R上的奇函数，且当x∈（-∞，0）时，xf′（x）＜f（-x）成立，若a=
f（
），b=（lg3）f（lg3），c=（log2
）f（log2
），则a，b，c大小关系（ ）
| 3 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、c＞a＞b |
| B、c＞b＞a |
| C、a＞b＞c |
| D、a＞c＞b |
等比数列{an}的各项是正数，且a3a11=16，则a7=（ ）
| A、±4 | B、4 | C、±2 | D、2 |
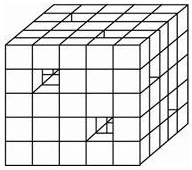如图所示，棱长为6的正方体无论从哪一个面看，都有两个直通的边长为l的正方形孔，则这个有孔正方体的表面积（含孔内各面）是（ ）| A、222 | B、258 |
| C、312 | D、324 |
设
=（
+
）+（
+
），
是任一非零向量，则下列结论中正确的为（ ）
①
∥
；
②
+
=
；
③
+
=
；
④|
+
|＜|
|+|
|；
⑤|
+
|=|
|+|
|．
| a |
| AB |
| CD |
. |
| BC |
| DA |
| b |
①
| a |
| b |
②
| a |
| b |
| a |
③
| a |
| b |
| b |
④|
| a |
| b |
| a |
| b |
⑤|
| a |
| b |
| a |
| b |
| A、①② | B、①③ |
| C、①③⑤ | D、③④⑤ |
已知⊙O：x2+y2=4，直线l：ax-y+1=0．则直线l与⊙O的位置关系是（ ）
| A、相交 | B、相离 |
| C、相切 | D、与a的值有关 |
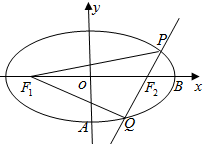已知椭圆