题目内容
在直角坐标系xOy中,曲线C1的参数方程为
(α为参数).在极坐标系中,C2的方程为ρ(3cosθ-4sinθ)=6,则C1与C2的交点的个数为 .
|
考点:圆的参数方程,简单曲线的极坐标方程
专题:直线与圆
分析:将曲线C1的参数方程转化为直角坐标方程为:x2+(y-2)2=1,将C2的极坐标方程ρ(3cosθ-4sinθ)=6化为直角坐标方程为:3x-4y-6=0,利用圆心到直线的距离与圆的半径比较即可.
解答:
解:∵曲线C1的参数方程为
(α为参数),
∴其直角坐标方程为:x2+(y-2)2=1;
又C2的极坐标方程为ρ(3cosθ-4sinθ)=6,
∴其直角坐标方程为:3x-4y-6=0;
∵圆C1的圆心(0,2)到直线3x-4y-6=0的距离d=
=
>1,
∴直线C2与圆C1相离,
∴C1与C2的交点的个数为0个,
故答案为:0.
|
∴其直角坐标方程为:x2+(y-2)2=1;
又C2的极坐标方程为ρ(3cosθ-4sinθ)=6,
∴其直角坐标方程为:3x-4y-6=0;
∵圆C1的圆心(0,2)到直线3x-4y-6=0的距离d=
| |3×0-4×2-6| | ||
|
| 14 |
| 5 |
∴直线C2与圆C1相离,
∴C1与C2的交点的个数为0个,
故答案为:0.
点评:本题考查圆的参数方程与直线的极坐标方程的应用,考查转化思想与点到直线间的距离的应用,属于中档题.

练习册系列答案
相关题目
已知集合A={x|(
)x<1},B={x|x2-3x-4>0},则A∩B等于( )
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
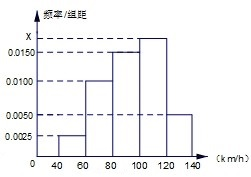 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有