题目内容
已知t是实数,求函数f(x)=x2+|x-t|-1的最小值.
考点:函数的最值及其几何意义
专题:计算题,压轴题,函数的性质及应用
分析:将函数化简为f(x)=
,分类讨论函数的最小值.
|
解答:
解:f(x)=x2+|x-t|-1=
,
①当t≥
时,
f(x)min=f(
)=t-
,
②当-
<t<
时,
f(x)min=f(t)=t2-1,
③当t≤-
时,
f(x)min=f(-
)=-t-
,
综上所述,
f(x)min=
.
|
①当t≥
| 1 |
| 2 |
f(x)min=f(
| 1 |
| 2 |
| 5 |
| 4 |
②当-
| 1 |
| 2 |
| 1 |
| 2 |
f(x)min=f(t)=t2-1,
③当t≤-
| 1 |
| 2 |
f(x)min=f(-
| 1 |
| 2 |
| 5 |
| 4 |
综上所述,
f(x)min=
|
点评:本题考查了分段函数的最小值的求法,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
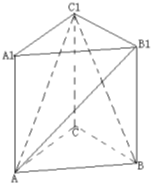 (文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.