题目内容
已知(3
-
)n的展开式中第三项为常数项,则展开式中个项系数的和为 .
| x |
| 1 | ||
|
考点:二项式系数的性质
专题:二项式定理
分析:利用二项展开式的通项公式求出通项,当r=3时x的指数为0,列出方程求出n,令二项式中的x=1,求出展开式各项的系数和.
解答:
解:(3
-
)n的展开式的第三项为:3n-2•
•x
•(-
)2=3n-2•
•x
-1
∴
-2=0,n=4.
令二项式中的x=1得到展开式的各项系数和为(3-1)4=16.
故展开式的各项系数和为16.
故答案为:16.
| x |
| 1 | ||
|
| C | 2 n |
| n-2 |
| 2 |
| 1 | ||
|
| C | 2 n |
| n-2 |
| 2 |
∴
| n |
| 2 |
令二项式中的x=1得到展开式的各项系数和为(3-1)4=16.
故展开式的各项系数和为16.
故答案为:16.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、考查通过赋值法求展开式的各项系数和.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
函数f(x)=
-
( )
| x |
| 1-2x |
| x |
| 2 |
| A、是偶函数,在(-∞,0)上是增函数 |
| B、是偶函数,在(-∞,0)上是减函数 |
| C、是奇函数,在(-∞,0)上是增函数 |
| D、是奇函数,在(-∞,0)上是减函数 |
在区间[-3,3]上任取两数x,y,使x2-y-1<0成立的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有
现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有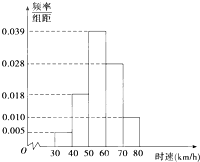 经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于
经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于