题目内容
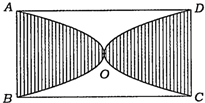 如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是
如图,矩形ABCD的面积为3,以矩形的中心O为顶点作两条抛物线,分别过点A、B和点C、D,若在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是考点:几何概型
专题:计算题,概率与统计
分析:以面积为测度,利用几何概型的概率公式,即可求得结论.
解答:
 解:以O为坐标原点,建立如图所示的坐标系,令开口向右的抛物线的方程为y2=2px(p>0),D(a,
解:以O为坐标原点,建立如图所示的坐标系,令开口向右的抛物线的方程为y2=2px(p>0),D(a,
),则
=2pa,
∴2p=
,
∴在第一象限的方程为y=
,
∴阴影部分的面积为4
dx=4
•
x
=2
∴落在阴影部分内的概率为
,
∴在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是200颗.
故答案为:200.
 解:以O为坐标原点,建立如图所示的坐标系,令开口向右的抛物线的方程为y2=2px(p>0),D(a,
解:以O为坐标原点,建立如图所示的坐标系,令开口向右的抛物线的方程为y2=2px(p>0),D(a,| 3 |
| 4a |
| 9 |
| 16a2 |
∴2p=
| 9 |
| 16a3 |
∴在第一象限的方程为y=
|
∴阴影部分的面积为4
| ∫ | a 0 |
|
|
| 2 |
| 3 |
| 3 |
| 2 |
| | | a 0 |
∴落在阴影部分内的概率为
| 2 |
| 3 |
∴在矩形ABCD中随机撒入300颗豆子,则落在阴影部分内的豆子大约是200颗.
故答案为:200.
点评:本题考查几何概型,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=
-
( )
| x |
| 1-2x |
| x |
| 2 |
| A、是偶函数,在(-∞,0)上是增函数 |
| B、是偶函数,在(-∞,0)上是减函数 |
| C、是奇函数,在(-∞,0)上是增函数 |
| D、是奇函数,在(-∞,0)上是减函数 |
| ∫ | 2 -1 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
将函数f(x)=sin(2x-
)的图象向右平移
个单位所得到的一条对称轴的方程是( )
| π |
| 6 |
| π |
| 3 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |
设[x]表示不大于x的最大整数,则函数y=[lgx-1]-2lgx+1的零点之积为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、-
|
 现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有
现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法种数共有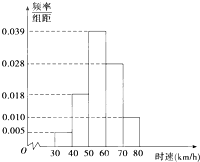 经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于
经过随机抽样获得100辆汽车经过某一雷达测速地区的时速(单位:km/h),并绘制成如图所示的频率分布直方图,其中这100辆汽车时速的范围是[30,80],数据分组为[30,40),[40,50),[50,60),[60,70),[70,80].设时速达到或超过60km/h的汽车有x辆,则x等于