题目内容
19.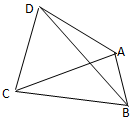 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{3}+1$ |
分析 运用余弦定理,表示出AC,进而用三角函数表示出S△BCD.
解答 解:在△ABC中,设∠ACB=α,∠ACB=β,由余弦定理得:
AC2=12+22-2×1×2cosα=5-4cosα,
∵△ACD为正三角形,
∴CD2=5-4cosα,
由正弦定理得:$\frac{1}{sinβ}$=$\frac{AC}{sinα}$,
∴AC•sinβ=sinα,
∴CD•sinβ=sinα,
∵(CD•cosβ)2=CD2(1-sin2β)=CD2-sin2α=5-4cosα-sin2α=(2-cosα)2,
∵β<∠BAC,
∴β为锐角,CD•cosβ=2-cosα,
∴S△BCD=$\frac{1}{2}$•2•CD•sin($\frac{π}{3}$+β)
=CD•sin($\frac{π}{3}$+β)
=$\frac{\sqrt{3}}{2}$CD•cosβ+$\frac{1}{2}$CD•sinβ
=$\frac{\sqrt{3}}{2}$•(2-cosα)+$\frac{1}{2}$sinα
=$\sqrt{3}$+sin(α-$\frac{π}{3}$),
当α=$\frac{5π}{6}$时,(S△BCD)max=$\sqrt{3}$+1.
故选:D.
点评 本题考查三角形的面积的最值的求法,注意运用余弦定理和面积公式,同时考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
9.若双曲线$\frac{x^2}{a^2}-{y^2}=1({a>0})$的一个焦点为(2,0),则a为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 5 | D. | 2 |
7.在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为( )
| A. | (x-1)2+y2=1 | B. | (x-1)2+y2=4 | C. | (x-1)2+y2=2 | D. | (x-1)2+y2=$\sqrt{2}$ |
2.已知a=9${\;}^{\frac{1}{3}}$,b=3${\;}^{\frac{2}{5}}$,c=4${\;}^{\frac{1}{5}}$,则( )
| A. | b<a<c | B. | a>b>c | C. | a<b<c | D. | c<a<b |