题目内容
2.已知a=9${\;}^{\frac{1}{3}}$,b=3${\;}^{\frac{2}{5}}$,c=4${\;}^{\frac{1}{5}}$,则( )| A. | b<a<c | B. | a>b>c | C. | a<b<c | D. | c<a<b |
分析 利用指数函数、对数函数的单调性直接求解.
解答 解:∵a=9${\;}^{\frac{1}{3}}$>b=3${\;}^{\frac{2}{5}}$=${9}^{\frac{1}{5}}$>c=4${\;}^{\frac{1}{5}}$,
∴a>b>c.
故选:B.
点评 本题考查三个数的大小的求法,是中档题,解题时要认真审题,注意指数函数、对数函数的单调性的合理运用.

练习册系列答案
相关题目
19.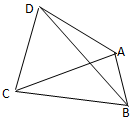 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{3}+1$ |
17.设等比数列{an}的前n项和为Sn,若a3=4,S3=7,则S6的值为( )
| A. | 31 | B. | 32 | C. | 63或$\frac{133}{27}$ | D. | 64 |
12.已知函数f(x)=ax3-3x的图象过点(-1,4),则实数a=( )
| A. | -2 | B. | 1 | C. | -1 | D. | 2 |
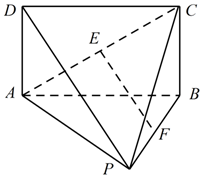 如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.
如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.