题目内容
10.已知函数f(x)=x2-(a+1)x+1(a∈R)(1)若关于x的不等式f(x)>0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)≤0的解集为P,集合Q={x|0≤x≤1},若P∩Q=∅,求实数a的取值范围.
分析 (1)应用一元二次不等式恒成立时判别式△≤0,求出a的取值范围;
(2)问题转化为不等式f(x)>0对x∈Q恒成立,由此求出a的取值范围.
解答 解:(1)∵f(x)=x2-(a+1)x+1(a∈R),
且关于x的不等式f(x)≥0的解集为R,
∴△=(a+1)2-4≤0,
解得-3≤a≤1,
∴实数a的取值范围是-3≤a≤1;
(2)∵关于x的不等式f(x)≤0的解集是P,
集合Q={x|0≤x≤1},当 P∩Q=∅时,
即不等式f(x)>0对x∈Q恒成立;
∴x∈[0,1]时,x2-(a+1)x+1>0恒成立,
∴a+1<x+$\frac{1}{x}$对于x∈(0,1]时恒成立;
∴a+1<2,
即a<1,
∴实数a的取值范围是a<1.
点评 本题考查了二次函数与一元二次方程以及对应不等式的解法与应用问题,考查了转化思想的应用问题,是综合性题目.

练习册系列答案
相关题目
20.若tan100°=a,则用a表示cos10°的结果为( )
| A. | $-\frac{1}{a}$ | B. | $-\frac{a}{{\sqrt{1+{a^2}}}}$ | C. | $\frac{a}{{\sqrt{1+{a^2}}}}$ | D. | $-\frac{1}{{\sqrt{1+{a^2}}}}$ |
1.在△ABC中,三个内角A,B,C的对边分别是a,b,c.若a=3,sinA=$\frac{1}{2}$,sin(A+C)=$\frac{3}{4}$,则b等于( )
| A. | 4 | B. | $\frac{8}{3}$ | C. | 6 | D. | $\frac{9}{2}$ |
5.已知α是第四象限角,sin($\frac{5π}{2}$+α)=$\frac{1}{5}$,那么tan α等于( )
| A. | -$\frac{2\sqrt{6}}{5}$ | B. | -2$\sqrt{6}$ | C. | 2$\sqrt{6}$ | D. | $\frac{2\sqrt{6}}{5}$ |
15.已知A,B,C三点不共线,点O为平面ABC外的一点,则下列条件中,能得到P∈平面ABC的是( )
| A. | $\overrightarrow{OP}=\frac{1}{3}\overrightarrow{OA}-\frac{2}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | B. | $\overrightarrow{OP}=\frac{2}{3}\overrightarrow{OA}+\frac{4}{3}\overrightarrow{OB}-\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | D. | $\overrightarrow{OP}=\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$ |
19.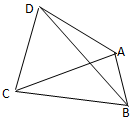 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{3}+1$ |
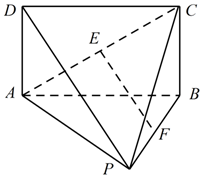 如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.
如图,在几何体P-ABCD中,平面ABCD⊥平面PAB,四边形ABCD为矩形,△PAB为正三角形,若AB=2,AD=1,E,F 分别为AC,BP中点.