题目内容
9.若双曲线$\frac{x^2}{a^2}-{y^2}=1({a>0})$的一个焦点为(2,0),则a为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 5 | D. | 2 |
分析 由题设条件知a2+1=4,a>0,即可求出a.
解答 解:由题设条件知a2+1=4,a>0,
∴a=$\sqrt{3}$,
故选B.
点评 本题考查双曲线的性质和应用,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若tan100°=a,则用a表示cos10°的结果为( )
| A. | $-\frac{1}{a}$ | B. | $-\frac{a}{{\sqrt{1+{a^2}}}}$ | C. | $\frac{a}{{\sqrt{1+{a^2}}}}$ | D. | $-\frac{1}{{\sqrt{1+{a^2}}}}$ |
17.已知F1,F2为双曲线C:x2-2y2=1的左右焦点,点P在双曲线C上,∠F1PF2=120°,则${S_{△P{F_1}{F_2}}}$=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
14.已知x、y的取值如表所示:
若y与x线性相关,且y=2x+a,则a=0.5.
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
1.在△ABC中,三个内角A,B,C的对边分别是a,b,c.若a=3,sinA=$\frac{1}{2}$,sin(A+C)=$\frac{3}{4}$,则b等于( )
| A. | 4 | B. | $\frac{8}{3}$ | C. | 6 | D. | $\frac{9}{2}$ |
19.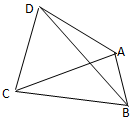 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
 如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )
如图所示,在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD面积的最大值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{3}+1$ |