题目内容
已知空间4个球，它们的半径分别为2，2，3，3，每个球都与其他三个球外切，另有一个小球与这4个球都外切，则这个小球的半径为 ．
考点：球的体积和表面积
专题：球
分析：设半径分别为3、3、2、2的四个球的球心分别为A、B、C、D，与这4个球都外切的小球球心为O，半径为r，其中AB=6，CD=4，AD=AC=BD=BC=5，连接OA、OB、OC、OD，取AB、CD中点F、G，连接OF、OG，求出FG，利用OF+OG=FG列出关于r的方程，求出这个小球的半径即可．
解答：
解：设半径分别为3、3、2、2的四个球的球心分别为A、B、C、D，与这4个球都外切的小球球心为O，半径为r，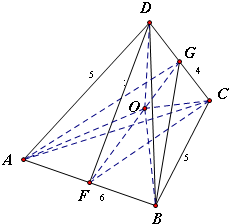
如图，连接AB、BC、CD、DA、AC、BD，得到四棱锥D-ABCD，
可得AB=6，CD=4，AD=AC=BD=BC=5，
连接OA、OB、OC、OD，取AB、CD中点F、G，连接OF、OG，
在等腰△ABC中，AC=BC=5，AF=BF=3，
所以CF=4，同理可得DF=4；
由此可得△CDF中，DF=CF，结合CG=DG，
连接FG，得FG是等腰△CDF底边中线，所以FG⊥CD
同理可得FG⊥AB，因此FG是异面直线AB、CD的公垂线段，
在Rt△AOF中，AF=3，OA=3+r，可得OF=
，同理，OG=
，
在Rt△CFG中，FG=
=2
，
所以OF+OG=FG，
即
+
=2
，
解之得r=
或r=-6（舍去），
则这个小球的半径为
．
故答案为：
．
如图，连接AB、BC、CD、DA、AC、BD，得到四棱锥D-ABCD，
可得AB=6，CD=4，AD=AC=BD=BC=5，
连接OA、OB、OC、OD，取AB、CD中点F、G，连接OF、OG，
在等腰△ABC中，AC=BC=5，AF=BF=3，
所以CF=4，同理可得DF=4；
由此可得△CDF中，DF=CF，结合CG=DG，
连接FG，得FG是等腰△CDF底边中线，所以FG⊥CD
同理可得FG⊥AB，因此FG是异面直线AB、CD的公垂线段，
在Rt△AOF中，AF=3，OA=3+r，可得OF=
| (r+3)2-9 |
| (r+2)2-4 |
在Rt△CFG中，FG=
| CF2-CG2 |
| 3 |
所以OF+OG=FG，
即
| (r+3)2-9 |
| (r+2)2-4 |
| 3 |
解之得r=
| 6 |
| 11 |
则这个小球的半径为
| 6 |
| 11 |
故答案为：
| 6 |
| 11 |
点评：本题主要考查了棱锥的结构特征，以及球的结构特征的运用，属于中档题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知复数z1=1+
i，z2=
cosθ+sinθi（θ∈[0，π]），z=z1•z2，则|z|的最大值是（ ）
| 3 |
| 3 |
| A、1 | ||
| B、2 | ||
| C、4 | ||
D、2
|
若点（1，2）和（1，1）在直线y-3x-m=0的两侧，则m的取值范围是（ ）
| A、-2＜m＜-1 |
| B、-2≤m≤-1 |
| C、m＜-2或m＞-1 |
| D、m≤-2或m≥-1 |