题目内容
13．
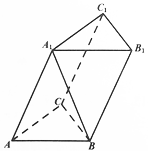在三棱柱ABC-A1B1C1中，△ABC是正三角形，且A1A=AB，顶点A1在底面ABC上的射影是△ABC的中心．（1）求证：AA1⊥BC；
（2）求直线A1B与平面BCC1B1所成角的大小．
分析 （1）由A1O⊥底面ABC，得A1O⊥BC，再由O是△ABC的中心，连接AO交BC于D，则AD⊥BC，由线面垂直的判定可得BC⊥平面A1AD，进一步得到AA1⊥BC；
（2）取B1C1的中点D1，连接A1D1，DD1，由（1）知，BC⊥平面ADD1A1，由线面垂直的判定和性质可得直线A1B与平面BCC1B1所成角．求解直角三角形得答案．
解答 （1）证明：如图，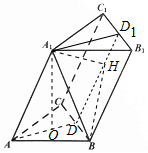
∵A1O⊥底面ABC，∴A1O⊥BC，
∵△ABC为正三角形，O为底面三角形的中心，
连接AO交BC于D，则AD⊥BC，
又AD∩A1D=O，∴BC⊥平面A1AD，
则AA1⊥BC；
（2）解：取B1C1的中点D1，连接A1D1，DD1，
由（1）知，BC⊥平面ADD1A1，
∴平面ADD1A1⊥平面BB1C1C，且平面ADD1A1∩平面BB1C1C=DD1，
过A1作A1H⊥DD1，垂足为H，连接BH，
则∠A1BH为直线A1B与平面BCC1B1所成角．
设A1A=AB=2a，可得${A}_{1}O=\frac{2\sqrt{6}}{3}a$，
由AD•A1O=AA1•A1H，得${A}_{1}H=\frac{AD•{A}_{1}O}{{A}_{1}A}=\frac{\sqrt{3}a•\frac{2\sqrt{6}}{3}a}{2a}$=$\sqrt{2}a$．
在Rt△A1HB中，sin$∠{A}_{1}BH=\frac{\sqrt{2}a}{2a}=\frac{\sqrt{2}}{2}$．
∴直线A1B与平面BCC1B1所成角为45°．
点评 本题考查线面垂直的判定和性质，考查了线面角的求法，考查空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
3．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的离心率是（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{5}{3}$ | C． | $\frac{{\sqrt{7}}}{4}$ | D． | $\frac{25}{16}$ |
1．下列函数中，既是偶函数，又是在区间（0，+∞）上单调递减的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=2|x| | C． | y=ln$\frac{1}{|x|}$ | D． | y=x2 |
8．已知m，n是两条不同的直线，α，β是两个不同的平面（ ）
| A． | 若m∥α，m∥β，则α∥β | B． | 若m⊥α，m∥β，则α∥β | C． | 若m⊥α，n∥α，则m∥n | D． | 若m⊥α，n⊥α，则m∥n |
5．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}），{F_1}$为左焦点，A为右顶点，B1，B2分别为上、下顶点，若F1，A，B1，B2四点在同一圆上，则此椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{3}-1}}{2}$ | B． | $\frac{{\sqrt{5}-1}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
2．已知函数f（x）的定义域为[0，2]，则函数$g（x）=f（{2x}）+\sqrt{8-{2^x}}$的定义域为（ ）
| A． | [0，1] | B． | [0，2] | C． | [1，2] | D． | [1，3] |