题目内容
4.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±2\sqrt{2}x$,则此双曲线的离心率等于3.分析 由双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±2\sqrt{2}x$,得到$\frac{b}{a}$=2$\sqrt{2}$,再根据离心率公式计算即可.
解答 解:由双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±2\sqrt{2}x$,
∴$\frac{b}{a}$=2$\sqrt{2}$,
∵e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+8}$=3,
故答案为:3.
点评 本题考查双曲线的方程和性质,主要考查双曲线的离心率的求法,属于基础题.

练习册系列答案
相关题目
14.已知直线l1:3x+2y+1=0,l2:x-2y-5=0,设直线l1,l2的交点为A,则点A到直线${l_0}:y=-\frac{3}{4}x-\frac{5}{2}$的距离为( )
| A. | 1 | B. | 3 | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\frac{{15\sqrt{7}}}{7}$ |
12.“k=1”是“直线$kx-y-3\sqrt{2}=0$与圆x2+y2=9相切”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
19.抛物线y=4x2的焦点到准线的距离是( )
| A. | 4 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
9.若直线x+y+m=0与圆x2+y2=m相切,则m的值是( )
| A. | 0或2 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$或2 |
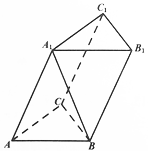 在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.
在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心. 如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.
如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.