题目内容
3．双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的离心率是（ ）| A． | $\frac{5}{4}$ | B． | $\frac{5}{3}$ | C． | $\frac{{\sqrt{7}}}{4}$ | D． | $\frac{25}{16}$ |
分析 根据双曲线方程求出a，c的值，根据离心率公式即可求出．
解答 解：由双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$可得a=4，c=5，
∴e=$\frac{c}{a}$=$\frac{5}{4}$，
故选：A
点评 本题考查双曲线的方程和性质，主要考查双曲线的离心率的求法，属于基础题．
练习册系列答案
相关题目
13．某公司的管理者通过公司近年来科研费用支出x（百万元）与公司所获得利润y（百万元）的散点图发现，y与x之间具有线性相关关系，具体数据如表：
（1）求y对x的回归直线方程；（参考数据：$\sum_{i=1}^{5}$x${\;}_{i}^{2}$=16.3，$\sum_{i=1}^{5}$xiyi=18.5）
（2）若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元，预测2017年该公司可获得的利润为多少万元？
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 科研费用x（百万元） | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
| 公司所获利润y（百万元） | 1 | 1.5 | 2 | 2.5 | 3 |
（2）若该公司的科研投入从2011年开始连续10年每一年都比上一年增加10万元，预测2017年该公司可获得的利润为多少万元？
14．已知直线l1：3x+2y+1=0，l2：x-2y-5=0，设直线l1，l2的交点为A，则点A到直线${l_0}：y=-\frac{3}{4}x-\frac{5}{2}$的距离为（ ）
| A． | 1 | B． | 3 | C． | $\frac{{5\sqrt{7}}}{7}$ | D． | $\frac{{15\sqrt{7}}}{7}$ |
11．直三棱柱ABC-A1B1C1的各顶点都在同一球面上，若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于（ ）
| A． | 20π | B． | 10π | C． | 5π | D． | 5$\sqrt{5}$π |
18．抛掷一枚质地均匀的骰子，向上的一面出现任意一种点数的概率都是$\frac{1}{6}$，记事件A为“向上的点数是奇数”，事件B为“向上的点数不超过3”，则概率P（A∪B）=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
8．一个几何体的三视图如图所示（单位：cm），则该几何体的表面积是（ ）
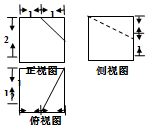
| A． | 4cm2 | B． | $\frac{43}{2}$cm2 | C． | 23cm2 | D． | 24cm2 |
12．“k=1”是“直线$kx-y-3\sqrt{2}=0$与圆x2+y2=9相切”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
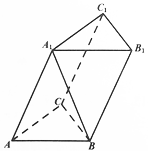在三棱柱ABC-A1B1C1中，△ABC是正三角形，且A1A=AB，顶点A1在底面ABC上的射影是△ABC的中心．