题目内容
2．已知函数f（x）的定义域为[0，2]，则函数$g（x）=f（{2x}）+\sqrt{8-{2^x}}$的定义域为（ ）| A． | [0，1] | B． | [0，2] | C． | [1，2] | D． | [1，3] |
分析 由已知f（x）的定义域求得f（2x）的定义域，结合根式内部的代数式大于等于0求得答案．
解答 解：∵函数f（x）的定义域为[0，2]，
∴由0≤2x≤2，解得0≤x≤1．
∴由$\left\{\begin{array}{l}{0≤x≤1}\\{8-{2}^{x}≥0}\end{array}\right.$，解得0≤x≤1．
∴函数$g（x）=f（{2x}）+\sqrt{8-{2^x}}$的定义域为[0，1]．
故选：A．
点评 本题考查函数的定义域及其求法，关键是掌握该类问题的求解方法，是基础题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
12．“k=1”是“直线$kx-y-3\sqrt{2}=0$与圆x2+y2=9相切”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
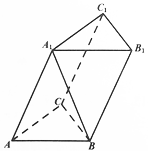在三棱柱ABC-A1B1C1中，△ABC是正三角形，且A1A=AB，顶点A1在底面ABC上的射影是△ABC的中心．
10．下列命题中假命题是（ ）
| A． | ?x0∈R，lnx0＜0 | B． | ?x∈（-∞，0），ex＞0 | ||
| C． | ?x＞0，5x＞3x | D． | ?x0∈（0，+∞），2＜sinx0+cosx0 |
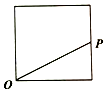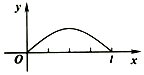
点P从点O出发，按逆时针方向沿周长为l的正方形运动一周，记O，P两点连线的距离y与点P走过的路程x为函数f（x），则y=f（x）的图象大致是（ ）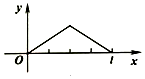
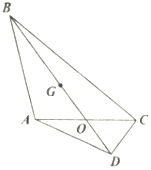如图，在平面四边形ABCD中，$\overrightarrow{BA}•\overrightarrow{BC}=32$．
如图，网格纸上每个小正方形的边长为1，若粗线画出的是某几何体的三视图，则此几何体的体积为10．
11．已知函数$f（x）=\sqrt{x}sinx$，则f'（π）=（ ）
| A． | $\sqrt{π}$ | B． | $-\sqrt{π}$ | C． | $\frac{{\sqrt{π}}}{2π}$ | D． | $\frac{{\sqrt{2π}}}{2π}$ |