题目内容
3.${(\frac{1}{2x}-\sqrt{x})^9}$的展开式中的常数项为$\frac{21}{2}$.(用数学作答)分析 通项公式Tr+1=$(\frac{1}{2})^{9-r}$(-1)r${∁}_{9}^{r}$${x}^{\frac{3}{2}r-9}$,令$\frac{3}{2}r-9$=0,解得r即可得出.
解答 解:通项公式Tr+1=${∁}_{9}^{r}(\frac{1}{2x})^{9-r}(-\sqrt{x})^{r}$=$(\frac{1}{2})^{9-r}$(-1)r${∁}_{9}^{r}$${x}^{\frac{3}{2}r-9}$,
令$\frac{3}{2}r-9$=0,解得r=6,
∴常数项为$(\frac{1}{2})^{3}$${∁}_{9}^{6}$=$\frac{21}{2}$.
故答案为:$\frac{21}{2}$.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
11.已知函数$f(x)=\sqrt{x}sinx$,则f'(π)=( )
| A. | $\sqrt{π}$ | B. | $-\sqrt{π}$ | C. | $\frac{{\sqrt{π}}}{2π}$ | D. | $\frac{{\sqrt{2π}}}{2π}$ |
18.阅读如图的程序框图,运行相应的程序,则输出的T的值为( )


| A. | 57 | B. | 120 | C. | 183 | D. | 247 |
8.设集合A={x|x2-x-6<0},B={x|-3≤x≤1},则A∪B等于( )
| A. | [-2,1) | B. | (-2,1] | C. | [-3,3) | D. | (-3,3] |
5.已知角α(0<α<$\frac{π}{2}$)的终边经过点(cos2β,1+sin3βcosβ-cos3βsinβ),($\frac{π}{2}$<β<π,且β≠$\frac{3π}{4}$),则α-β=( )
| A. | -$\frac{7π}{4}$ | B. | -$\frac{3π}{4}$ | C. | -$\frac{π}{4}$ | D. | $\frac{5π}{4}$ |
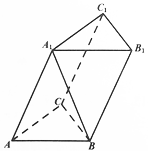 在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.
在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心. 如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.
如图,网格纸上每个小正方形的边长为1,若粗线画出的是某几何体的三视图,则此几何体的体积为10.