题目内容
9.已知a>0,则${∫}_{-a}^{a}$(xcosx-5sinx+2)dx=4a.分析 利用导数的运算法则和微积分基本定理即可得出.
解答 解:方法一:∵(xsinx+6cosx+2x)′=xcosx-5sinx+2,
∴${∫}_{-a}^{a}$(xcosx-5sinx+2)dx=(xcosx-5sinx+2)|${\;}_{-a}^{a}$=4a.
方法二:∵y=xcosx-5sinx为奇函数
${∫}_{-a}^{a}$(xcosx-5sinx)dx+${∫}_{-a}^{a}$2dx=0+2x|${\;}_{-a}^{a}$=4a,
故答案为:4a
点评 本题考查了导数的运算法则和微积分基本定理的应用问题,是基础题目.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.设集合A={x|x2-x-6<0},B={x|-3≤x≤1},则A∪B等于( )
| A. | [-2,1) | B. | (-2,1] | C. | [-3,3) | D. | (-3,3] |
5.已知圆锥的底面半径为1,侧面展开图的圆心角为60°,则此圆锥的表面积为( )
| A. | 3π | B. | 5π | C. | 7π | D. | 9π |
14.方程xy2+x2y=1所表示的曲线( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
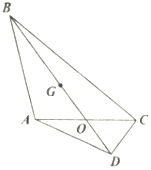 如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.