题目内容
已知f（x）=f（x-1）+f（x+1）且f（0）=0，则f（2010）= ．
考点：抽象函数及其应用,函数的值
专题：函数的性质及应用
分析：f（x）=f（x-1）+f（x+1）①根据条件得到f（x+1）=f（x）+f（x+2）②，由①+②得f（x+3）=-f（x），继而得到f（x+6）=f（x），得到函数为周期函数，问题得以解决．
解答：
解：因为f（x）=f（x-1）+f（x+1）
所以f（x+1）=f（x）+f（x+2）
两式相加得0=f（x-1）+f（x+2）
即：f（x+3）=-f（x）
∴f（x+6）=f（x）
∴f（x）是以6为周期的周期函数
∵2010=6×335
∴f（2010）=f（0）=0，
故答案为：0
所以f（x+1）=f（x）+f（x+2）
两式相加得0=f（x-1）+f（x+2）
即：f（x+3）=-f（x）
∴f（x+6）=f（x）
∴f（x）是以6为周期的周期函数
∵2010=6×335
∴f（2010）=f（0）=0，
故答案为：0
点评：本题是一道抽象函数问题，解题的关键是巧妙的赋值，求出函数值和函数的周期性，再利用周期性求函数值，即灵活的“赋值法”是解决抽象函数问题的基本方法
练习册系列答案
名校课堂系列答案
相关题目
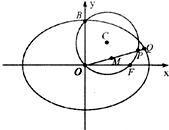已知圆C经（x-1）2+（y-2）2=5经过椭圆E：
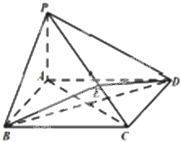如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．PA=1，AD=2．
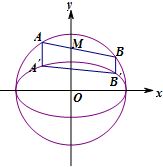如图，设AB、A′B′分别是圆O：x2+y2=4和椭圆C：已知正项等比数列{an}满足a7=a6+2a5．若存在两项am，an使得
=4a1，则
+
的最小值为（ ）
| aman |
| 1 |
| m |
| 9 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|