题目内容
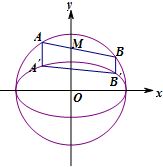 如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:
如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:| x2 |
| 4 |
(1)若弦A′B′所在直线斜率为-1,且弦A′B′的中点的横坐标为
| 4 |
| 5 |
(2)若弦AB过定点M(0,
| 3 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得:直线A′B′的方程为y=-x+m,与椭圆的方程联立得到根与系数的关系,再利用中点坐标公式即可得出.
(2)解法一:由(Ⅰ)得:圆O的方程为:x2+y2=4.设A(x1,y1),B(x2,y2),A′(x1,m),
B′(x2,n),利用点A在圆O上,可得
+
=4.利用点A′在椭圆C上,可得
+m2=1.利用弦AB过定点M(0,
),可得x1≠x2且kAM=kBM,利用点斜式可得直线A′B′,即可证明.
解法二:由(Ⅰ)得:圆O的方程为:x2+y2=4.设A(x1,y1)、B(x2,y2),根据圆O上的每一点横坐标不变,纵坐标缩短为原来的
倍可得到椭圆C,又端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号,可得A′(x1,
)、B′(x2,
),由弦AB过定点M(0,
),猜想弦A′B′过定点M′(0,
).由于弦AB过定点M(0,
),可得x1≠x2且kAM=kBM,证明kA′M′=kB′M′即可.
(2)解法一:由(Ⅰ)得:圆O的方程为:x2+y2=4.设A(x1,y1),B(x2,y2),A′(x1,m),
B′(x2,n),利用点A在圆O上,可得
| x | 2 1 |
| y | 2 1 |
| ||
| 4 |
| 3 |
| 2 |
解法二:由(Ⅰ)得:圆O的方程为:x2+y2=4.设A(x1,y1)、B(x2,y2),根据圆O上的每一点横坐标不变,纵坐标缩短为原来的
| 1 |
| 2 |
| y1 |
| 2 |
| y2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
解答:
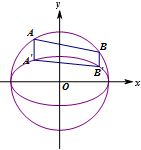 解:(1)由题意得:直线A′B′的方程为y=-x+m
解:(1)由题意得:直线A′B′的方程为y=-x+m
⇒5x2-8mx+4m2-4=0,
△=80-16m2>0,
∴设A′(x1,y1),B′(x2,y2),
∴
=
=
,解得m=1.
将m=1代入△检验符合题意,
故满足题意的直线A′B′方程为:y=-x+1.
(2)解法一:由(Ⅰ)得:圆O的方程为:x2+y2=4.
设A(x1,y1),B(x2,y2),A′(x1,m),B′(x2,n),
∵点A在圆O上,∴
+
=4,…①
∵点A′在椭圆C上,∴
+m2=1,…②
联立方程①②解得:m=
,同理解得:n=
.
∴A′(x1,
)、B′(x2,
),
∵弦AB过定点M(0,
),
∴x1≠x2且kAM=kBM,即
=
,
化简得
=
,
直线A′B′的方程为:y-
=
(x-x1),即y=
x+
,
由
=
得直线A′B′的方程为:y=
x+
,
∴弦A′B′必过定点M′(0,
).
解法二:由(Ⅰ)得:圆O的方程为:x2+y2=4.
设A(x1,y1)、B(x2,y2),
∵圆O上的每一点横坐标不变,纵坐标缩短为原来的
倍可得到椭圆C,
又端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号,
∴A′(x1,
)、B′(x2,
)
由弦AB过定点M(0,
),猜想弦A′B′过定点M′(0,
).
∵弦AB过定点M(0,
),
∴x1≠x2且kAM=kBM,即
=
…①
kA′M′=
=
,kB′M′=
=
,
由①得kA′M′=kB′M′,
∴弦A′B′必过定点M′(0,
).
 解:(1)由题意得:直线A′B′的方程为y=-x+m
解:(1)由题意得:直线A′B′的方程为y=-x+m
|
△=80-16m2>0,
∴设A′(x1,y1),B′(x2,y2),
∴
| x1+x2 |
| 2 |
| 4m |
| 5 |
| 4 |
| 5 |
将m=1代入△检验符合题意,
故满足题意的直线A′B′方程为:y=-x+1.
(2)解法一:由(Ⅰ)得:圆O的方程为:x2+y2=4.
设A(x1,y1),B(x2,y2),A′(x1,m),B′(x2,n),
∵点A在圆O上,∴
| x | 2 1 |
| y | 2 1 |
∵点A′在椭圆C上,∴
| ||
| 4 |
联立方程①②解得:m=
| y1 |
| 2 |
| y2 |
| 2 |
∴A′(x1,
| y1 |
| 2 |
| y2 |
| 2 |
∵弦AB过定点M(0,
| 3 |
| 2 |
∴x1≠x2且kAM=kBM,即
y1-
| ||
| x1 |
y2-
| ||
| x2 |
化简得
| y1x2-y2x1 |
| x2-x1 |
| 3 |
| 2 |
直线A′B′的方程为:y-
| y1 |
| 2 |
| ||||
| x2-x1 |
| 1 |
| 2 |
| y2-y1 |
| x2-x1 |
| y1x2-y2x1 |
| 2(x2-x1) |
由
| y1x2-y2x1 |
| x2-x1 |
| 3 |
| 2 |
| 1 |
| 2 |
| y2-y1 |
| x2-x1 |
| 3 |
| 4 |
∴弦A′B′必过定点M′(0,
| 3 |
| 4 |
解法二:由(Ⅰ)得:圆O的方程为:x2+y2=4.
设A(x1,y1)、B(x2,y2),
∵圆O上的每一点横坐标不变,纵坐标缩短为原来的
| 1 |
| 2 |
又端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号,
∴A′(x1,
| y1 |
| 2 |
| y2 |
| 2 |
由弦AB过定点M(0,
| 3 |
| 2 |
| 3 |
| 4 |
∵弦AB过定点M(0,
| 3 |
| 2 |
∴x1≠x2且kAM=kBM,即
y1-
| ||
| x1 |
y2-
| ||
| x2 |
kA′M′=
| ||||
| x1 |
| 1 |
| 2 |
y1-
| ||
| x1 |
| ||||
| x2 |
| 1 |
| 2 |
y2-
| ||
| x2 |
由①得kA′M′=kB′M′,
∴弦A′B′必过定点M′(0,
| 3 |
| 4 |
点评:本题考查了直线与椭圆圆相交问题转化为方程联立可得根与系数的关系,考查了椭圆与圆的变换关系,考查了直线过定点问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设定义域为R的函数f(x)满足f(x+1)=
+
,且f(-1)=
,则f(2014)的值为( )
| 1 |
| 2 |
| f(x)-[f(x)]2 |
| 1 |
| 2 |
| A、-1 | ||
| B、1 | ||
| C、2014 | ||
D、
|
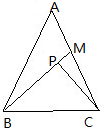 如图,在△ABC中,AB=AC=3
如图,在△ABC中,AB=AC=3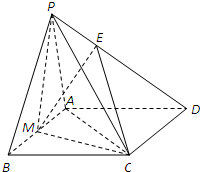 在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.
在四棱锥P-ABCD中,PA=PB.底面ABCD是菱形,且∠ABC=60°.E在棱PD上,满足PE=2DE,M是AB的中点.