题目内容
18．函数$y=\frac{2}{x}+ln\frac{1}{x-1}$的零点所在的大致区间是（ ）| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
分析 利用函数的零点判定定理推出结果即可．
解答 解：函数$y=\frac{2}{x}+ln\frac{1}{x-1}$，函数是连续减函数，
f（2）=1+ln1=1＞0，
f（3）=$\frac{2}{3}$+ln$\frac{1}{2}$=$\frac{2}{3}-ln2$=ln$\frac{\root{3}{{e}^{2}}}{2}$＜0．
因为f（2）f（3）＜0，
所以函数$y=\frac{2}{x}+ln\frac{1}{x-1}$的零点所在的大致区间是（2，3）．
故选：C．
点评 本题考查函数的零点判定定理的应用，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．不等式|2a-b|+|a+b|≥|a|（|x-1|+|x+1|）对于任意不为0的实数a，b恒成立，则实数x的范围为（ ）
| A． | $（-∞，-\frac{1}{2}]∪[\frac{1}{2}，+∞）$ | B． | $[-\frac{1}{2}，\frac{1}{2}]$ | C． | $（-∞，-\frac{3}{2}]∪[\frac{3}{2}，+∞）$ | D． | $[-\frac{3}{2}，\frac{3}{2}]$ |
13．设回归方程$\widehat{y}$=7-3x，当变量x增加两个单位时（ ）
| A． | y平均增加3个单位 | B． | y平均减少3个单位 | ||
| C． | y平均增加6个单位 | D． | y平均减少6个单位 |
3．已知函数$f（x）=\frac{1}{3}{x^3}-{x^2}+ax-5$在[-1，2]上不单调，则实数a的取值范围是（ ）
| A． | [-3，1） | B． | （-3，0） | C． | （-3，1） | D． | （-3，1] |
7．已知数列{an}满足a1=60，an+1-an=2n，则$\frac{{a}_{n}}{n}$的最小值为（ ）
| A． | $\frac{29}{2}$ | B． | 2$\sqrt{60}$ | C． | $\frac{29}{4}$ | D． | $\frac{102}{7}$ |
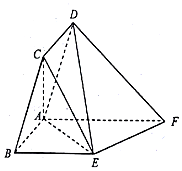如图，在平行四边形ABCD中，AB=1，BC=2，∠ABC=60°，在直角梯形ABEF中，BE=2，AF=3，BE∥AF，∠BAF=90°，平面ABCD⊥平面ABEF．