题目内容
8.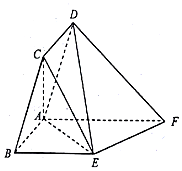 如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.(Ⅰ)求证:AC⊥平面ABEF;
(Ⅱ)求证:CD∥平面AEF;
(Ⅲ)求三棱锥D-AEF的体积.
分析 (Ⅰ)推导出AB⊥AC,由此利用平面ABCD⊥平面ABEF,能证明AC⊥平面ABEF.
(Ⅱ)求出CD∥AB,由此能证明CD∥平面AEF.
(Ⅲ)由V三棱锥D-AEF=V三棱锥C-AEF,能求出三棱锥D-AEF的体积.
解答 证明:(Ⅰ)∵在△ABC中,AB=1,BC=2,∠ABC=60°,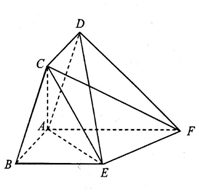
∴AC2=AB2+BC2-2AB•BC•cos∠ABC
=${1}^{2}+{2}^{2}-2×1×2×\frac{1}{2}$=3,
∴AC2+AB2=BC2,∴AB⊥AC,
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,
且AC?平面ABCD,
∴AC⊥平面ABEF.
(Ⅱ)∵四边形ABCD是平行四边形,
∴CD∥AB,
∵CD?平面ABEF,AB?平面ABEF,
∴CD∥平面AEF.
解:(Ⅲ)连结CF,由(Ⅱ)知CD∥平面AEF,
∴点D到平面AEF的距离等于点C到平面AEF的距离,
由(Ⅰ)知AC=$\sqrt{3}$,
∴三棱锥D-AEF的体积V三棱锥D-AEF=V三棱锥C-AEF=$\frac{1}{3}×(\frac{1}{2}×3×1)×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查线面垂直、线面平行的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
18.函数$y=\frac{2}{x}+ln\frac{1}{x-1}$的零点所在的大致区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
20.已知集合P={x|1≤x≤3},Q={x|x2≥4},则P∩(∁RQ)=( )
| A. | [2,3] | B. | (-2,3] | C. | [1,2) | D. | (-∞,-2]∪[1,+∞) |
18.已知函数f(x)=lnx+ln(2-x),则( )
| A. | f(x)在(0,2)单调递增 | B. | f(x)在(0,2)单调递减 | ||
| C. | y=f(x)的图象关于直线x=1对称 | D. | y=f(x)的图象关于点(1,0)对称 |