题目内容
1.已知函数f(x)=lnx+x与函数$g(x)=\frac{b}{x}+{x^2}$有交点,则实数b的取值范围是( )| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
分析 求出函数的定义域,结合函数有交点,转化为方程有根,利用参数分离法,结合导数研究函数的取值范围进行求解即可.
解答 解:函数f(x)的定义域为(0,+∞),
若函数f(x)=lnx+x与函数$g(x)=\frac{b}{x}+{x^2}$有交点,
则等价为$g(x)=\frac{b}{x}+{x^2}$=lnx+x,则(0,+∞)上有解,
即b=-x3+x2+xlnx,
设h(x)=-x3+x2+xlnx=x(-x2+x+lnx),
则m(x)=-x2+x+lnx,
则m′(x)=-2x+1+$\frac{1}{x}$=$\frac{-2{x}^{2}+x+1}{x}$=$\frac{-(x-1)(2x+1)}{x}$,
由m′(x)=$\frac{-(x-1)(2x+1)}{x}$>0得0<x<1,
由m′(x)=$\frac{-(x-1)(2x+1)}{x}$<0得x>1,
即当x=1时,函数m(x)取得极大值,同时也是最大值,m(1)=-1+1+ln1=0,
即当x>0时,m(x)=-x2+x+lnx≤0,
则当x>0时,h(x)=-x3+x2+xlnx=x(-x2+x+lnx)≤0,
若b=-x3+x2+xlnx有交点,
则b≤0,
故选:B.
点评 本题主要考查函数与方程的应用,利用方程和函数之间的关系,利用参数分离法,结合导数研究函数的性质是解决本题的关键.

练习册系列答案
相关题目
11.已知集合A={x|y=ln(1-2x)},B={x|x2≤x},全集U=A∪B,则∁U(A∩B)=( )
| A. | (-∞,0) | B. | (-$\frac{1}{2}$,1] | C. | (-∞,0)∪[$\frac{1}{2}$,1] | D. | (-$\frac{1}{2}$,0] |
16.若复数z满足$({1+i})\cdotz=i$,则此复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
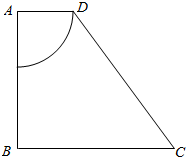 如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.
如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.