题目内容
11.已知集合A={x|y=ln(1-2x)},B={x|x2≤x},全集U=A∪B,则∁U(A∩B)=( )| A. | (-∞,0) | B. | (-$\frac{1}{2}$,1] | C. | (-∞,0)∪[$\frac{1}{2}$,1] | D. | (-$\frac{1}{2}$,0] |
分析 化简集合A、B,写出U以及A∩B和∁U(A∩B).
解答 解:集合A={x|y=ln(1-2x)}={x|1-2x>0}={x|x<$\frac{1}{2}$}=(-∞,$\frac{1}{2}$),
B={x|x2≤x}={x|x(x-1)≤0}={x|0≤x≤1}=[0,1],
∴U=A∪B=(-∞,1],
∴A∩B=[0,$\frac{1}{2}$);
∴∁U(A∩B)=(-∞,0)∪[$\frac{1}{2}$,1].
故选:C.
点评 本题考查了集合的有关定义与运算问题,是基础题目.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
16.不等式2log2(x-3)<log24x的解集为( )
| A. | ∅ | B. | (1,9) | C. | (-∞,1)∪(9,+∞) | D. | (3,9) |
20.已知i,j,k是空间直角坐标系O-xyz的单位正交基底,并且$\overrightarrow{AB}$=-i+j-k,则B点的坐标为( )
| A. | (-1,1,-1) | B. | (-i,j,-k) | C. | (1,-1,-1) | D. | 不确定 |
1.已知函数f(x)=lnx+x与函数$g(x)=\frac{b}{x}+{x^2}$有交点,则实数b的取值范围是( )
| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
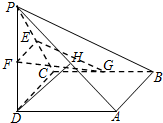 如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB,E,F,G,H分别为PC、PD、BC、PA的中点.