题目内容
10.已知函数f(x)=ex(Ⅰ)证明:当x≠0时,(1-x)f(x)<1;
(Ⅱ)证明:当a≠b时,$\frac{f(a)-f(b)}{a-b}$<$\frac{f(a)+f(b)}{2}$.
分析 (Ⅰ)先构造函数g(x)=(1-x)f(x),根据导数和函数最值的关系即可证明;
(Ⅱ)不防设a<b,记g(x)=[f(x)+f(a)](x-a)-2[f(x)-f(a)],分别两次求导,求出函数的最值,即可证明.
解答 证明:(Ⅰ)设g(x)=(1-x)f(x)=(1-x)ex,
∴g′(x)=-xex,
当g′(x)>0时,即x<0,函数g(x)单调递增,
当g′(x)<0时,即x>0,函数g(x)单调递减,
∴g(x)max≥g(0)=1,
∴当x≠0时,(1-x)f(x)<1;
(Ⅱ)不防设a<b
记g(x)=[f(x)+f(a)](x-a)-2[f(x)-f(a)],x≥a
∴g'(x)=f'(x)(x-a)+[f(x)+f(a)]-2f'(x),
=f'(x)(x-a)-[f(x)-f(a)],
∴g″(x)=f″(x)(x-a)+f'(x)-f'(x)=f(x)(x-a)>0,
∴g'(x)在x>a上单调增加,
则g'(x)>g'(a)=0,
∴g(x)在x>a上单调增加,
又g(x)可在x=a处连续,
∴g(x)>g(a)=0,
即[f(x)+f(a)](x-a)-2[f(x)-f(a)]>0,
特别的取x=b,[f(b)+f(a)](b-a)-2[f(b)-f(a)]>0,
整理得$\frac{f(a)-f(b)}{a-b}$<$\frac{f(a)+f(b)}{2}$,
问题得以证明.
点评 本题考查了导数和函数的最值得关系,以及转化思想,构造函数是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知i,j,k是空间直角坐标系O-xyz的单位正交基底,并且$\overrightarrow{AB}$=-i+j-k,则B点的坐标为( )
| A. | (-1,1,-1) | B. | (-i,j,-k) | C. | (1,-1,-1) | D. | 不确定 |
1.已知函数f(x)=lnx+x与函数$g(x)=\frac{b}{x}+{x^2}$有交点,则实数b的取值范围是( )
| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
15.定义在R上的奇函数f(x),当x∈(-∞,0)时xf(x)递减,若a=3f(3),b=(logπ3)•f(logπ3),c=-2f(-2),则a,b,c的大小关系( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<c<a |
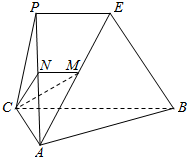 如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.
如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.