题目内容
11.已知f(x)是定义在[-2,2]上的奇函数,且g(x)=f(x)+6,f(-2)=4,当a,b∈[-2,2],a+b≠0时,恒有(a+b)[f(a)+f(b)]<0成立.(Ⅰ)求g(2)的值;
(Ⅱ)判断f(x)在[-2,2]上的单调性(不用证明);
(Ⅲ)若g(x)≤m2-2km+2对所有的k∈[-1,1]恒成立,求实数m的取值范围.
分析 (Ⅰ)根据函数奇偶性的关系即可求g(2)的值;
(Ⅱ)根据抽象函数的关系即可判断f(x)在[-2,2]上的单调性(不用证明);
(Ⅲ)根据函数恒成立,转化为以k为主变量的函数,进行求解即可.
解答 解:(Ⅰ)∵f(-2)=4,∴f(=-2)=-f(2)=4,即f(2)=-4,
则g(2)=f(2)+6=-4+6=2.
(Ⅱ)f(x)在[-2,2]上的单调性(不用证明);
∵当a,b∈[-2,2],a+b≠0时,恒有(a+b)[f(a)+f(b)]<0成立,
∴此时函数f(x)为减函数.
(Ⅲ)若g(x)≤m2-2km+2对所有的k∈[-1,1]恒成立,
则f(x)+6≤m2-2km+2对所有的k∈[-1,1]恒成立,
即f(x)≤m2-2km-4对所有的k∈[-1,1]恒成立,
∵函数f(x)在[-2,2]上为减函数,
∴函数f(x)的最大值为f(-2)=4,
即4≤m2-2km-4对所有的k∈[-1,1]恒成立,
即m2-2km-8≥0对所有的k∈[-1,1]恒成立
即-2mk+m2-8≥0对所有的k∈[-1,1]恒成立,
设h(k)=-2mk+m2-8,
则$\left\{\begin{array}{l}{h(-1)≥0}\\{h(1)≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{{m}^{2}+2m-8≥0}\\{{m}^{2}-2m-8≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥2或m≤-4}\\{m≥4或m≤-2}\end{array}\right.$,
即m≥4或m≤-4.
点评 本题主要考查抽象函数的应用,以及函数恒成立问题,利用参数转化法是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
1.已知函数f(x)=lnx+x与函数$g(x)=\frac{b}{x}+{x^2}$有交点,则实数b的取值范围是( )
| A. | (-∞,1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
2.某校高一学生1500人,高二学生1200人,高三学生1300人,为了调查高中各年级学生的寒假学习计划,决定采用分层抽样法抽取200人进行调查,则应从高二年级抽取的人数为( )
| A. | 75 | B. | 65 | C. | 60 | D. | 40 |
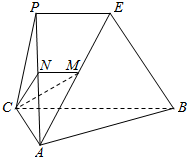 如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.
如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.