题目内容
求y=
+x（k＞0）的单调区间．
| k2 |
| x |
考点：利用导数研究函数的单调性,基本不等式
专题：计算题,导数的综合应用
分析：由题意先求定义域，再求导y′=1-
=
；从而确定函数的单调区间．
| k2 |
| x2 |
| (x+k)(x-k) |
| x2 |
解答：
解：y=
+x的定义域为{x|x≠0}；
y′=1-
=
；
则由y′＞0得，x＞k或x＜-k；
由y′＜0得，-k＜x＜0或0＜x＜k；
故y=
+x（k＞0）的单调增区间为（-∞，-k），（k，+∞）；
单调减区间为（-k，0），（0，k）．
| k2 |
| x |
y′=1-
| k2 |
| x2 |
| (x+k)(x-k) |
| x2 |
则由y′＞0得，x＞k或x＜-k；
由y′＜0得，-k＜x＜0或0＜x＜k；
故y=
| k2 |
| x |
单调减区间为（-k，0），（0，k）．
点评：本题考查了导数的综合应用，注意k＞0，属于中档题．
练习册系列答案
相关题目
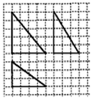如图，格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体最长的棱的长度等于（ ）A、
| ||
B、
| ||
C、5
| ||
D、2
|
函数f（x）=
，若f（2）+f（α）=e+1，则α的所有可能值为（ ）
|
| A、1 | ||||
B、-
| ||||
C、1或-
| ||||
D、1或
|