题目内容
已知椭圆C的方程为
+
=1，直线l0：x=4，A是椭圆C的右顶点，点P（x1，y1）是椭圆上异于左，右顶点的一个动点，直线PA与l0交于点M1，直线l过点P且与椭圆交于另一点B（x2，y2），与l0交于点M2，
（1）若直线l经过椭圆的左焦点F，且使得
•
=3，求直线l的方程；
（2）若点B恰为椭圆的左顶点，同x轴上是否存在定点D，使得变化的点P，以M1M2为直径的圆总经过点D，若存在，求这样的圆面积的最小值；若不存在；请说明理由．
| x2 |
| 4 |
| y2 |
| 3 |
（1）若直线l经过椭圆的左焦点F，且使得
| AP |
| AB |
（2）若点B恰为椭圆的左顶点，同x轴上是否存在定点D，使得变化的点P，以M1M2为直径的圆总经过点D，若存在，求这样的圆面积的最小值；若不存在；请说明理由．
考点：椭圆的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：（1）设PB方程为y=k（x+1）（k≠0）代入椭圆方程，得（3+4k2）x2+8k2x+4k2-12=0，由此利用韦达定理结合已知条件，结合向量的数量积坐标表示表示，能求出直线l的方程；
（2）假设存在x轴上定点D，使得以M1M2为直径的圆恒过点D，设出D的坐标，求出AP和PB的方程，取x=4得到
M1，M2的坐标，写出向量
和
的坐标，由数量积等于0列式求出D的坐标．
（2）假设存在x轴上定点D，使得以M1M2为直径的圆恒过点D，设出D的坐标，求出AP和PB的方程，取x=4得到
M1，M2的坐标，写出向量
| DM1 |
| DM2 |
解答：
（1）解：由于直线PB的斜率存在，设PB方程为y=k（x+1）（k≠0）
代入椭圆的方程
+
=1，得（3+4k2）x2+8k2x+4k2-12=0，
由P（x1，y1），B（x2，y2），
得x1+x2=-
，x1x2=
，
y1y2=k2（x1+1）（x2+1）=k2（x1x2+x1+x2+1）=
，
•
=（x1-2）（x2-2）+y1y2=x1x2-2（x1+x2）+4+y1y2
=
=3，
解得，k=±
，
故直线l的方程为y=±
（x+1）；
（2）假设存在x轴上定点D，使得以M1M2为直径的圆恒过点D．
设P（x1，y1），D（m，0），
则
+
=1，得12y12=36-9x12．kAP=
，kBP=
，
椭圆右准线为x=4．
所以AP方程为：y=
（x-2），则M1（4，
），
PB方程为：y=
（x+2），则M2（4，
）．
则
=（4-m，
），
=（4-m，
）．
由以M1M2为直径的圆总经过点D，得
•
=0，
即有（4-m）2+
=0，
即（4-m）2=9，解得m=1或m=7．
所以存在x轴上定点D（1，0）或（7，0），使得以M1M2为直径的圆恒过点D．
代入椭圆的方程
| x2 |
| 4 |
| y2 |
| 3 |
由P（x1，y1），B（x2，y2），
得x1+x2=-
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
y1y2=k2（x1+1）（x2+1）=k2（x1x2+x1+x2+1）=
| -9k2 |
| 3+4k2 |
| AP |
| AB |
=
| 27k2 |
| 3+4k2 |
解得，k=±
| ||
| 5 |
故直线l的方程为y=±
| ||
| 5 |
（2）假设存在x轴上定点D，使得以M1M2为直径的圆恒过点D．
设P（x1，y1），D（m，0），
则
| x12 |
| 4 |
| y12 |
| 3 |
| y1 |
| x1-2 |
| y1 |
| x1+2 |
椭圆右准线为x=4．
所以AP方程为：y=
| y1 |
| x1-2 |
| 2y1 |
| x1-2 |
PB方程为：y=
| y1 |
| x1+2 |
| 6y1 |
| x1+2 |
则
| DM1 |
| 2y1 |
| x1-2 |
| DM2 |
| 6y1 |
| x1+2 |
由以M1M2为直径的圆总经过点D，得
| DM1 |
| DM2 |
即有（4-m）2+
| 12y12 |
| x12-4 |
即（4-m）2=9，解得m=1或m=7．
所以存在x轴上定点D（1，0）或（7，0），使得以M1M2为直径的圆恒过点D．
点评：本题考查了椭圆的标准方程和性质，考查了直线和椭圆的位置关系，训练了平面向量的数量积判断两个向量的垂直，考查了学生的计算能力，是有一定难度题目．
练习册系列答案
相关题目
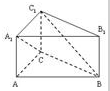已知直三棱柱ABC--A1B1C1中，AB=4，AC=AA1=2，∠ACB=90°．