题目内容
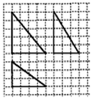如图，格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体最长的棱的长度等于（ ）A、
| ||
B、
| ||
C、5
| ||
D、2
|
考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：根据几何体的三视图，得出该几何体是什么图形，从而求出结果．
解答：
解：根据几何体的三视图知，
该几何体为三棱锥，
底面△ABC为俯视图中的直角三角形，∠BAC=90°，
其中AC=4，AB=3，BC=5，PB⊥底面ABC，且PB=5，
∴∠PBC=∠PBA=90°，
∴最长的棱为PC，
在Rt△PBC中，由勾股定理得，
PC=
=
=5
．
故选：C．
解：根据几何体的三视图知，该几何体为三棱锥，
底面△ABC为俯视图中的直角三角形，∠BAC=90°，
其中AC=4，AB=3，BC=5，PB⊥底面ABC，且PB=5，
∴∠PBC=∠PBA=90°，
∴最长的棱为PC，
在Rt△PBC中，由勾股定理得，
PC=
| PB2+BC2 |
| 52+32+42 |
| 2 |
故选：C．
点评：本题考查了空间几何体的三视图的应用问题，解题的关键是由三视图得出几何体是什么图形，是基础题目．
练习册系列答案
相关题目
如图的程序运行之后输出值为16，那么输入的值x应该是（ ）
| A、3或-3 | B、-5 |
| C、5或-3 | D、5或-5 |
观察以下不等式：1＞
；1+
+
＞1；1+
+
…+
＞
；1+
+
+…+
＞2；1+
+
+…+
＞
；由此推测第n个不等式为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 7 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 31 |
| 5 |
| 2 |
A、1+
| ||||||||
B、1+
| ||||||||
C、1+
| ||||||||
D、1+
|