题目内容
19.数列{an}满足a1+a2+a3+…an=2n-an(n∈N+).数列{bn}满足bn=$\frac{2-n}{2}({{a_n}-2})$,则{bn}中的最大项的值是$\frac{1}{8}$.分析 由已知数列递推式可得,数列{an-2}构成以$\frac{1}{2}$为公比的等比数列,求出其通项公式后代入bn=$\frac{2-n}{2}({{a_n}-2})$,再由数列的函数特性求得{bn}中的最大项的值.
解答 解:由a1+a2+a3+…an=2n-an,得Sn=2n-an,
取n=1,求得a1=1;
由Sn=2n-an,得Sn-1=2(n-1)-an-1(n≥2),
两式作差得an=2-an+an-1,即${a}_{n}-2=\frac{1}{2}({a}_{n-1}-2)$(n≥2),
又a1-2=-1≠0,
∴数列{an-2}构成以$\frac{1}{2}$为公比的等比数列,
则${a}_{n}-2=-1×(\frac{1}{2})^{n-1}$,
则bn=$\frac{2-n}{2}({{a_n}-2})$=$\frac{2-n}{2}•(-\frac{1}{{2}^{n-1}})=\frac{n-2}{{2}^{n}}$,
当n=1时,${b}_{1}=-\frac{1}{2}$,当n=2时,b2=0,当n=3时,${b}_{3}=\frac{1}{8}$,
而当n≥3时,$\frac{{b}_{n+1}}{{b}_{n}}=\frac{\frac{n-1}{{2}^{n+1}}}{\frac{n-2}{{2}^{n}}}=\frac{n-1}{2(n-2)}≤1$,
∴{bn}中的最大项的值是$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,考查数列的函数特性,是中档题.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
7.二项式${(ax-\frac{{\sqrt{3}}}{6})^3}$(a>0)的展开式的第二项的系数为-$\frac{{\sqrt{3}}}{2}$,则$\int_{-2}^a{x^2}$dx的值为( )
| A. | 3或$\frac{7}{3}$ | B. | $\frac{7}{3}$ | C. | 3 | D. | 3或$-\frac{10}{3}$ |
14.已知复数z满足$\frac{2z+m}{z-3}=i$,且z的实部与虚部之和为0,则实数m等于( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
4.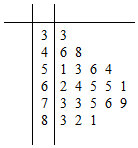 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
附:
(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
11.若i是虚数单位,复数z满足(1-i)z=1,则|2z-3|=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
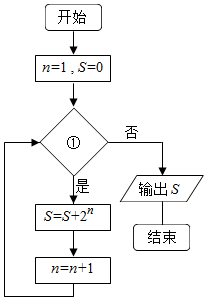
8.若如图所示的程序框图输出的S是126,则条件①可以为( )

| A. | n≤5 | B. | n≤6 | C. | n≤7 | D. | n≤8 |