题目内容
15.对于集合A={(x,y)|$\left\{\begin{array}{l}{x+y≤2}\\{x-y≤4}\\{x≥1}\end{array}\right.$}.命题p:至少存在一个点(x0,y0)∈A,使得代数式y0=2${\;}^{{x}_{0}-m}$-1成立,则实数m的取值范围为[1,3].分析 画出满足条件的平面区域,显然y=2x-m-1恒过(m,-1)这个点,问题转化为点(m,-1)在线段AB上即可,从而求出m的范围即可.
解答 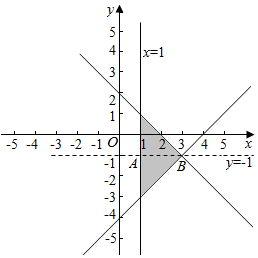 解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
由$\left\{\begin{array}{l}{y=-1}\\{x=1}\end{array}\right.$得A(1,-1),由$\left\{\begin{array}{l}{x=1}\\{x-y=4}\\{x+y=2}\end{array}\right.$得B(1,3),
连结AB,
显然y=2x-m-1恒过(m,-1)这个点,
若至少存在一个点(x0,y0)∈A,使得代数式y0=2${\;}^{{x}_{0}-m}$-1成立,
只需(m,-1)在线段AB上即可,
∴1≤m≤3,
故答案为:[1,3].
点评 本题考查了简单的线性规划问题,问题转化为点(m,-1)在线段AB上是解题的关键,本题是一道中档题.

练习册系列答案
相关题目
6.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,过点F作x轴的垂线交双曲线的右支于C,D两点,与双曲线的渐近线交于点P,点C和点P在第-象限,点D在第四象限,若|PC|=|CD|,则该双曲线的离心率为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{9}{8}$ |
20.从集合A={-2,-1,2}中随机选取一个数记为a,从集合B={-1,1,3}中随机选取一个数记为b,则直线ax-y+b=0不经过第四象限的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{4}$ |
7.二项式${(ax-\frac{{\sqrt{3}}}{6})^3}$(a>0)的展开式的第二项的系数为-$\frac{{\sqrt{3}}}{2}$,则$\int_{-2}^a{x^2}$dx的值为( )
| A. | 3或$\frac{7}{3}$ | B. | $\frac{7}{3}$ | C. | 3 | D. | 3或$-\frac{10}{3}$ |
4.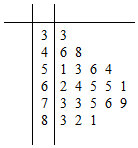 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
附:
(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.