题目内容
15.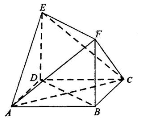 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.(1)求证:AE∥平面BFC
(2)若AD⊥DE,AD=DE=1,AB=2,∠BDA=60°,求三棱锥F-AEC的体积.
分析 (1)推导出AD∥BC,从而AD∥平面BCF,推导出DE∥BF,从而DE∥平面BCF,进而平面ADE∥平面BCF,由此能证明AE∥平面BCF.
(2)设AC∩BD=O,则O为AC中点,连结OE,OF,则VF-ABC=VC-AEF=2VO-AEF=2VA-OEF,由此能求出三棱锥F-AEC的体积.
解答 证明:(1)∵面ABCD是平行四边形,∴AD∥BC,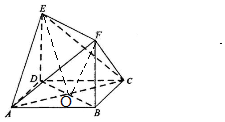
∵AD?平面BCF,BC?平面BCF,
∴AD∥平面BCF,
∵四边形BDEF是矩形,∴DE∥BF,
∵DE?平面BCF,BF?平面BCF,
∴DE∥平面BCF,
∵AD∩DE=D,AD?平面ADE,DE?平面ADE,
∴平面ADE∥平面BCF,
∵AE?平面ADE,∴AE∥平面BCF.
解:(2)设AC∩BD=O,则O为AC中点,连结OE,OF,
则VF-ABC=VC-AEF=2VO-AEF=2VA-OEF,
在△ABD中,∠BAD=60°,AD=1,AB=2,
由余弦定理得BD2=AB2+AD2-2AB•AD•cos∠BAD,
∴BD=$\sqrt{3}$,
∴AB2=AD2+BD2,∴AD⊥BD,
∵DE⊥AD,BD∩DE=D,BD?平面BDEF,DE?平面BDEF,
∴AD⊥平面BDEF,
故AD为A到平面BDEF的距离,
∵DE=1,∴S△OEF=$\frac{1}{2}{S}_{四边形BDEF}$=$\frac{1}{2}×OD×EE=\frac{\sqrt{3}}{2}$,
∴VA-OEF=$\frac{1}{3}{S}_{△OEF}•AD$=$\frac{\sqrt{3}}{6}$,
∴三棱锥F-AEC的体积VF-AEC=2VA-OEF=$\frac{\sqrt{3}}{3}$.
点评 本题考查几何体的体积及直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查考查推理论证能力、运算求解能力、空间想象能力,考查化归转化思想、函数与方程思想,数形结合思想,是中档题.

①($\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$ ②(cosx)′=-sinx ③(2x)′=2xln2 ④(lgx)′=$\frac{-1}{xln10}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
(1)残差就是随机误差
(2)残差图的纵坐标是残差
(3)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越高
(4)残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越低.
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (2)(4) |
| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
| A. | 10$\sqrt{5}$km | B. | 10$\sqrt{7}$km | C. | 10$\sqrt{3}$km | D. | 30km |
| A. | 充分而不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
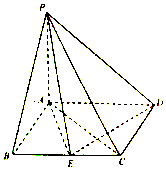 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.