题目内容
20.已知数列{an}满足a1=4,an+1=an+2n,设bn=$\frac{{a}_{n}}{n}$,若存在正整数T,使得对一切n∈N*,bn≥T恒成立,则T的最大值为( )| A. | 1 | B. | 2 | C. | 4 | D. | 3 |
分析 利用累加法求出数列的通项公式,再根据基本不等式求出bn的范围,即可求出T的范围.
解答 解:∵an+1=an+2n,
∴an+1-an=2n,
∴a2-a1=2,
a3-a2=4,
…
an-an-1=2(n-1),
累加可得an-a1=2(1+2+3+…+n-1)=n(n-1),
∴an=n(n-1)+4,
∴bn=$\frac{{a}_{n}}{n}$=n-1+$\frac{4}{n}$≥2$\sqrt{n•\frac{4}{n}}$-1=4-1=3,当且仅当n=2时取等号,
∴T≤3,
∴T的最大值为3,
故选:D
点评 本题考查了数列的递推关系式和通项公式的求法和基本不等式的应用,属于中档题

练习册系列答案
相关题目
10.已知f(x)为偶函数,在[0,+∞)上f(x)=$\left\{\begin{array}{l}{a({x}^{3}-1),x∈[0,1]}\\{x+\frac{a}{x}-2,x∈(1,+∞)}\end{array}\right.$且为单调递增函数,则使得f(ax)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
8.某大学餐饮中心为了了解新生的饮食习惯,利用简单随机抽样的方法在全校一年级学生中进行了抽样调查,调查结果如表所示:
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 20 | 80 |
| 北方学生 | 10 | 10 | 20 |
| 合计 | 70 | 30 | 100 |
(2)根据(1)的结论,你能否提出更好的调查方法来了解该校大学新生的饮食习惯,说明理由.
5.某市政府在调查市民收入增减与旅游愿望的关系时,采用独立性检验法抽查了3000人,计算发现K2的观测者k=6.023,根据这一数据查阅如表:
得到的正确结论是( )
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.5 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有97.5%以上的把握认为“市民收入增减与旅游愿望无关” | |
| B. | 有97.5%以上的把握认为“市民收入增减与旅游愿望有关” | |
| C. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望无关” | |
| D. | 在犯错误的概率不超过0.25%的前提下,认为“市民收入增减与旅游愿望有关” |
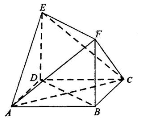 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.