题目内容
6．以下式子正确的个数是（ ）①（$\frac{1}{x}$）′=$\frac{1}{{x}^{2}}$ ②（cosx）′=-sinx ③（2x）′=2xln2 ④（lgx）′=$\frac{-1}{xln10}$．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据题意，依次对四个式子的函数求导，即可得判断其是否正确，即可得答案．
解答 解：根据题意，依次分析四个式子：
对于①、$\frac{1}{x}$=x-1，则（$\frac{1}{x}$）′=（x-1）′=-$\frac{1}{{x}^{2}}$，故①错误；
对于②、（cosx）′=-sinx 正确；
对于③、（2x）′=2xln2，正确；
对于④、（lgx）′=$\frac{1}{xln10}$，故④错误；
综合可得：②③正确；
故选：B．
点评 本题考查导数的计算，关键是掌握导数的计算公式．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
17．已知集合A={x|x＞0}，B={x|x2-2x-3＜0}，则A∩B=（ ）
| A． | （-1，0） | B． | （0，3） | C． | （-∞，0）∪（3，+∞） | D． | （-1，3） |
14．若等差数列{an}的前n项和Sn满足S4≤4，S6≥12，则a4的最小值为（ ）
| A． | 2 | B． | $\frac{7}{2}$ | C． | 3 | D． | $\frac{5}{2}$ |
1．已知f（x）=$\frac{e^x}{{{x^2}+a}}（{a＞0}）$的两个极值点分别为x1，x2（x1＜x2），则a（lnx1+lnx2）的取值范围是（ ）
| A． | $[{-\frac{1}{e}，0}）$ | B． | （0，+∞） | C． | （0，1） | D． | $[{-\frac{1}{e}，+∞}）$ |
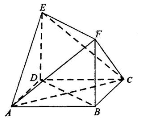在如图所示的多面体中，面ABCD是平行四边形，四边形BDEF是矩形．
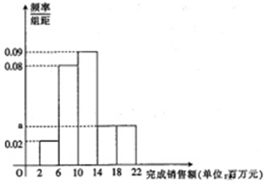某家电公司销售部门共有200位销售员，每位部门对每位销售员都有1400万元的年度销售任务，已知这200位销售员去年完成销售额都在区间[2，22]（单位：百万元）内，现将其分成5组，第1组，第2组，第3组，第4组，第5组对应的区间分别为[2，6），[6，10），[10，14），[14，18），[18，22]，绘制出频率分布直方图．