题目内容
4.两座灯塔A和B与海洋观察站C的距离分别为10km和20km,灯塔A在观察站C的北偏东15°方向上,灯塔B在观察站C的南偏西75°方向上,则灯塔A与灯塔B的距离为( )| A. | 10$\sqrt{5}$km | B. | 10$\sqrt{7}$km | C. | 10$\sqrt{3}$km | D. | 30km |
分析 先根据题意确定∠ACB的值,再由余弦定理可直接求得|AB|的值.
解答 解:由题意可知,∠ACB=180°+15°+90°-75°=120°,
AC=10km,BC=20km,
由余弦定理,得:AB=$\sqrt{100+400-2×10×20×(-\frac{1}{2})}$=10$\sqrt{7}$km.
故选B.
点评 本题主要考查余弦定理的应用.正弦定理和余弦定理在解三角形和解决实际问题时用的比较多,这两个定理及其推论,一定要熟练掌握并要求能够灵活应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若等差数列{an}的前n项和Sn满足S4≤4,S6≥12,则a4的最小值为( )
| A. | 2 | B. | $\frac{7}{2}$ | C. | 3 | D. | $\frac{5}{2}$ |
19.(3-2x-x4)(2x-1)6的展开式中,含x3项的系数为( )
| A. | 600 | B. | 360 | C. | -600 | D. | -360 |
13.高二(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为8,22,50的同学在样本中,那么还有一个同学的学号应为( )
| A. | 32 | B. | 33 | C. | 35 | D. | 36 |
11.设F1,F2是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{2}}=1$(0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
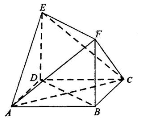 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
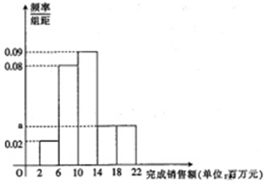 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.