题目内容
7.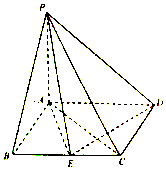 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.(1)证明:PE⊥ED;
(2)求二面角E-PD-A的大小.
分析 (1)在△ABC中,由题意可得△ABE为正三角形,则AE=1,在△AED中,求解三角形可得AE⊥ED.然后利用线面垂直的判定可得ED⊥平面PAE,从而得到PE⊥ED;
(2)由PA⊥平面ABCD,得平面PAD⊥平面ABCD,然后找出二面角E-PD-A的平面角.求解三角形可得二面角E-PD-A的大小.
解答 (1)证明:如图,
在△ABC中,∵AB=1,BC=2,AB⊥AC,
∴cosB=$\frac{1}{2}$,$∠\\;=60°$B=60°,又E为BC的中点,
∴△ABE为正三角形,则AE=1,
在△AED中,∵AE=1,AD=2,∠EAD=60°,
∴$E{D}^{2}={1}^{2}+{2}^{2}-2×1×2×\frac{1}{2}=3$,
∴AE2+ED2=AD2,则AE⊥ED.
又PA⊥平面ABCD,∴PA⊥ED,
∵PA∩AE=A,∴ED⊥平面PAE,则PE⊥ED;
(2)解:∵PA⊥平面ABCD,∴平面PAD⊥平面ABCD,
过E作EG⊥AD,垂足为G,则EG⊥平面PAD,∴EG⊥PD,
过G作GH⊥PD,垂足为H,连接EH,
∴PD⊥平面EGH,则PD⊥EH.
则∠EHG为二面角E-PD-A的平面角.
在Rt△AED中,由AE=1,AD=2,ED=$\sqrt{3}$,可得EG=$\frac{AE•ED}{AD}=\frac{\sqrt{3}}{2}$,
∴GD=$\sqrt{(\sqrt{3})^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{3}{2}$,
由△PAD∽△GHD,可得$\frac{GH}{GD}=\frac{PA}{PD}$,即GH=$\frac{PA•GD}{PD}=\frac{\frac{\sqrt{2}}{2}•\frac{3}{2}}{\sqrt{(\frac{\sqrt{2}}{2})^{2}+{2}^{2}}}$=$\frac{1}{2}$.
∴tan$∠EHG=\frac{EG}{GH}=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=\sqrt{3}$,即∠EHG=60°.
∴二面角E-PD-A的大小为60°.
点评 本题考查空间中直线与直线的位置关系,考查空间角的求法,关键是找出二面角的平面角,是中档题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 600 | B. | 360 | C. | -600 | D. | -360 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
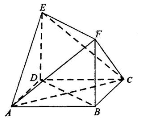 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.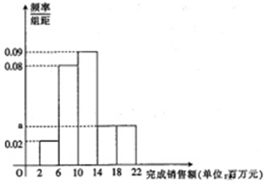 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.