题目内容
5.已知$f(x)=x{e^{ax}}-\frac{a}{2}{x^2}$-x+1,a≠0(Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若?x0>1,使$f({x_0})<\frac{a}{2}$成立,求参数a的取值范围.
分析 (Ⅰ)代入a值,求出导函数,找出极值点,得出函数的单调区间即可;
(Ⅱ)由题意即$f{(x)_{min}}<\frac{a}{2}$,当a>0时,f(x)min=f(1),当a<0,$f(1)>\frac{a}{2}$恒成立,由此利用导数性质能求出参数a的取值范围.
解答 解:(Ⅰ)$f(x)=x{e^x}-\frac{x^2}{2}-x+1$,
f'(x)=ex+xex-x-1=(ex-1)(x+1)=0时x1=0,x2=-1
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | - | + | ||
| f(x) | 增 | 减 | 增 |
(Ⅱ)由题意即$f{(x)_{min}}<\frac{a}{2}$,
x>1时,f'(x)=(ax+1)(eax-1)=0,
∴${x_1}=-\frac{1}{a}$,x2=0
当a>0时,
∵x>1,
∴f'(x)>0,
∴f(x)单调递增,
即f(x)min=f(1),f(1)=ea-$\frac{a}{2}$<$\frac{a}{2}$即ea-a<0,
设g(a)=ea-a,
a≥0时,g'(x)=ea-1≥0,
∴g(x)min=g(1)=1>0即ea>a恒成立,∴无解
当a<0时:
| x | (-∞,0) | 0 | $({0,-\frac{1}{a}})$ | $-\frac{1}{a}$ | $({-\frac{1}{a},+∞})$ |
| g'(x) | + | - | + | ||
| g(x) | ↑ | ↓ | ↑ |
若?x0>1使$f({x_0})<\frac{a}{2}$则$-\frac{1}{a}>!$且$f({-\frac{1}{a}})<\frac{a}{2}$$-\frac{1}{a}>1⇒$-1<a<0①,
$f({-\frac{1}{a}})=-\frac{1}{ae}$$+\frac{1}{2a}+1<\frac{a}{2}$${({a-1})^2}<2-\frac{2}{e}$$1-\sqrt{2-\frac{2}{e}}<a$$<1+\sqrt{2-\frac{2}{e}}$②,
由①②取交集,得参数a的取值范围:{a|$1-\sqrt{2-\frac{2}{e}}<a<0$}.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知f(x)为偶函数,在[0,+∞)上f(x)=$\left\{\begin{array}{l}{a({x}^{3}-1),x∈[0,1]}\\{x+\frac{a}{x}-2,x∈(1,+∞)}\end{array}\right.$且为单调递增函数,则使得f(ax)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,1) | D. | D、(-∞,$-\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
17.已知集合A={x|x>0},B={x|x2-2x-3<0},则A∩B=( )
| A. | (-1,0) | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-1,3) |
14.若等差数列{an}的前n项和Sn满足S4≤4,S6≥12,则a4的最小值为( )
| A. | 2 | B. | $\frac{7}{2}$ | C. | 3 | D. | $\frac{5}{2}$ |
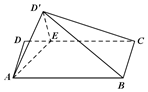 如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.
如图,矩形ABCD中,AB=4,AD=2,E在DC边上,且DE=1,将△ADE沿AE折到△AD'E的位置,使得平面AD'E⊥平面ABCE.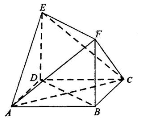 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.