题目内容
5.已知函数f(x)=x2+$\frac{a}{x}$,则“a<2”是“函数f(x)在(1,+∞)上为增函数”的( )| A. | 充分而不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分必要条件的定义及函数的单调性,得出a≤2,从而得出结论.
解答 解:∵f(x)=x2+$\frac{a}{x}$,
∴f′(x)=2x-$\frac{a}{{x}^{2}}$,
∵函数f(x)在(1,+∞)上为增函数,
∴2x-$\frac{a}{{x}^{2}}$>0在(1,+∞)恒成立,
∴a<2x3,
∴a≤2,
∴“a<2”是“函数f(x)在(1,+∞)上为增函数”充分不必要条件,
故选:A
点评 本题的考点是四种条件的判断、函数的单调性,充要条件的判断,通常先看谁能推出谁,再作判断,属基本题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
13.高二(1)班共有56人,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本,已知学号为8,22,50的同学在样本中,那么还有一个同学的学号应为( )
| A. | 32 | B. | 33 | C. | 35 | D. | 36 |
20.已知向量$\overrightarrow{a}$=(x,3),$\overrightarrow{b}$=(2,-2),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=( )
| A. | 5 | B. | $\sqrt{26}$ | C. | 2$\sqrt{5}$ | D. | 10 |
17.数列{an}的通项公式为${a_n}=\;\;|n-c|\;\;(\;n∈{N^*}\;)$.则“c≤1”是“{an}为递增数列”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设F1,F2是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{2}}=1$(0<b<2)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF2|+|BF2|最大值为5,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.设$z=\frac{i}{1-i}$(i为虚数单位),则$\frac{1}{|z|}$=( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
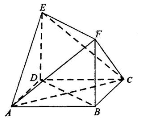 在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.
在如图所示的多面体中,面ABCD是平行四边形,四边形BDEF是矩形.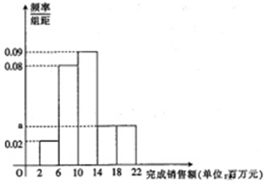 某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.
某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间[2,22](单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为[2,6),[6,10),[10,14),[14,18),[18,22],绘制出频率分布直方图.